已知函数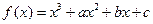
在
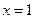与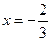
时，都取得极值。
（1）求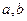
的值；
（2）若
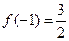，求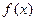
的单调区间和极值；
（3）若对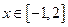
都有
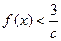恒成立，求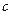
的取值范围。
如图，
是抛物线为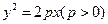
上的一点，以S为圆心，r为半径（
）做圆，分别交x轴于A，B两点，连结并延长SA、SB，分别交抛物线于C、D两点。
（1）求证：直线CD的斜率为定值；
（2）延长DC交x轴负半轴于点E，若EC : ED =" 1" : 3，求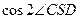
的值。
设函数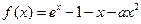
。
（1）若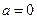
，求
的单调区间；
（2）若当
时，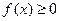
，求a的取值范围。
设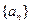
的公差大于零的等差数列，已知
，
.
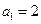（1）求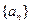的通项公式；
（2）设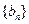
是以函数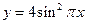
的最小正周期为首项，以
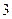为公比的等比数列，求数列
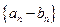的前
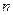项和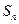
.
某普通高中共有教师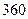
人，分为三个批次参加研修培训，在三个批次中男、女教师人数如下表所示：
| 第一批次 |
第二批次 |
第三批次 |
|
| 女教师 |
 |
 |
 |
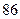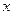| 男教师 |
 |
 |
 |
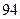已知在全体教师中随机抽取1名，抽到第二、三批次中女教师的概率分别是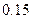
、
．
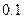（1）求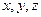
的值；
（2）为了调查研修效果，现从三个批次中按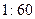
的比例抽取教师进行问卷调查，三个批次被选取的人数分别是多少？
（3）若从（2）中选取的教师中随机选出两名教师进行访谈，求参加访谈的两名教师“分别来自两个批次”的概率．
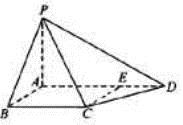
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.
（1）求证：CE⊥平面PAD；
（2）若PA=AB=1，AD=3，CD=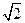
，∠CDA=45°，求四棱锥P-ABCD的体积.