（本小题满分12分）提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度v（单位：千米/小时）是车流密度x（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数
（1）当0≤x≤200时，求函数v（x）的表达式
（2）当车流密度x为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）f（x）＝x·v（x）可以达到最大，并求出最大值．（精确到1辆/小时）
为了测量两山顶 间的距离，飞机沿水平方向在 两点进行测量， 在同一个铅垂平面内（如示意图），飞机能够测量的数据有俯角和 间的距离，请设计一个方案，包括：①指出需要测量的数据（用字母表示，并在图中标出）；②用文字和公式写出计算M，N间的距离的步骤.
已知f（x）、g（x）是定义在［a，b］上的函数，若对任意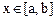
，总有
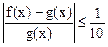，则称f（x）可被g（x）替代，试判断函数
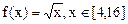能否被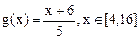
替代，并说明理由．
已知函数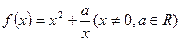
（1）判断函数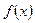
的奇偶性；
（2）若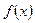在区间
是增函数，求实数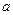
的取值范围．
设函数
上满足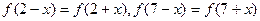
，且在闭区间[0，7]上，只有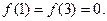
（1）试判断函数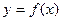
的奇偶性；
（2）试求方程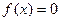
在闭区间[－2005，2005]上的根的个数，并证明你的结论．
某蔬菜基地种植番茄，由历年市场行情得知，从二月一日起的300天内，番茄市场售价与上市时间的关系用图（1）的一条折线表示；番茄的种植成本与上市时间的关系用图（2）的抛物线表示.
（1）写出图1表示的市场售价与时间的函数关系式P＝f（t）；图2表示的种植成本与时间的函数关系式Q＝g（t）；
（2）市场售价减去种植成本为纯收益，问何时上市的番茄纯收益最大?（注：市场售价和种植成本的单位：元／102，ｋg，时间单位：天）