(12分) 双曲线的两条渐近线的方程为y=±x,且经过点(3,-2).(1)求双曲线的方程;(2)过双曲线的右焦点F且倾斜角为60°的直线交双曲线于A、B两点,求|AB|.
本题共有3个小题,第1小题满分5分,第2小题满分8分,第3小题满分5分.
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆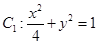 .
.
(1)若椭圆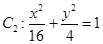 ,判断
,判断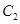 与
与 是否相似?如果相似,求出
是否相似?如果相似,求出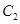 与
与 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
(2)写出与椭圆 相似且焦点在
相似且焦点在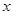 轴上、短半轴长为
轴上、短半轴长为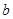 的椭圆
的椭圆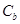 的标准方程;若在椭圆
的标准方程;若在椭圆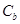 上存在两点
上存在两点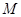 、
、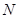 关于直线
关于直线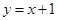 对称,求实数
对称,求实数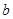 的取值范围;
的取值范围;
(3)如图:直线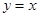 与两个“相似椭圆”
与两个“相似椭圆”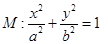 和
和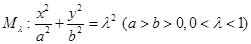 分别交于点
分别交于点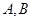 和点
和点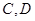 ,试在椭圆
,试在椭圆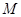 和椭圆
和椭圆 上分别作出点
上分别作出点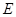 和点
和点 (非椭圆顶点),使
(非椭圆顶点),使 和
和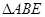 组成以
组成以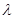 为相似比的两个相似三角形,写出具体作法.(不必证明)
为相似比的两个相似三角形,写出具体作法.(不必证明)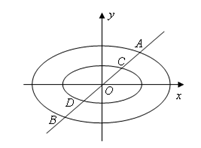
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
如图,圆锥的轴截面为等腰直角三角形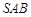 ,
,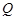 为底面圆周上一点.
为底面圆周上一点.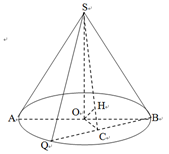
(1)如果 的中点为
的中点为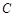 ,
,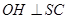 ,求证:
,求证: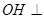 平面
平面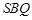 ;
;
(2)如果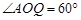 ,
,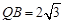 ,求此圆锥的体积;
,求此圆锥的体积;
(3)如果二面角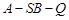 大小为
大小为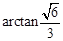 ,求
,求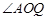 的大小.
的大小.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知圆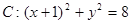 .
.
(1)求过点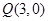 的圆C的切线
的圆C的切线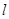 的方程;
的方程;
(2)如图,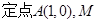 为圆C上一动点,点P在AM上,点N在CM上,且满足
为圆C上一动点,点P在AM上,点N在CM上,且满足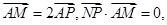 求
求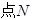 的轨迹.
的轨迹.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
在二项式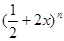 的展开式中:
的展开式中:
(1)若第5项,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项;
(2)若所有项的二项式系数和等于4096,求展开式中系数最大的项.
如图,直线 平面
平面 ,
, 为正方形,
为正方形, ,求直线
,求直线 与
与 所成角的大小.
所成角的大小.