(本题满分14分
某工厂生产一种产品的成本费由三部分组成
①职工工资固定支出 元
元
②原材料费每件40元
③电力与机器保养等费用为每件 元,其中
元,其中 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费 (元)表示成产品件数
(元)表示成产品件数 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量 不超过
不超过 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价 与产品件数
与产品件数 有如下关系:
有如下关系: ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
(本小题满分10分)设函数 (其中
(其中 >
>
0, ),且
),且 的图象在y轴右侧的第一个最高点的横坐标为
的图象在y轴右侧的第一个最高点的横坐标为 .
.
(1)求 的最小正周期;
的最小正周期;
(2)如果 在区间
在区间 上的最小值为
上的最小值为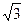 ,求a的值.
,求a的值.
(本小题满分10分)已知
 =
= ,
, =
= ,
,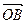 =
= ,设
,设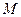 是直
是直
线 上一点,
上一点, 是坐标原点
是坐标原点
⑴求使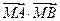 取最小值时的
取最小值时的 ;
; 
⑵对(1)中的点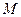 ,求
,求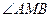 的余弦值。
的余弦值。
(本小题满分8分)已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、
黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)列出一次任取2个球的所有基本事件;
(3)从中取2个球,求至少有一个红球的概率.
(本小题满分8分)已知角 的终边在
的终边在 上,求
上,求
(1) 的值;
的值;
(2)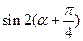 的值.
的值.
已知二次函数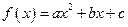 满足条件:①
满足条件:① 是
是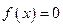 的两个零点;②
的两个零点;②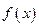 的最小值为
的最小值为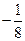
(1)求函数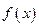 的解析式;
的解析式;
(2)设数列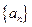 的前
的前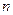 项积为
项积为 ,且
,且 ,
,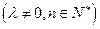 ,求数列
,求数列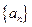 的前
的前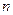 项和
项和
(3)在(2)的条件下,当 时,若
时,若 是
是 与
与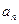 的等差中项,试问数列
的等差中项,试问数列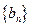 中
中
第几项的值最小?并求出这个最小值。