(本小题满分l2分)
若函数y=为奇函数.
(1)求a的值;
(2)求函数的定义域;
(3)讨论函数的单调性.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米。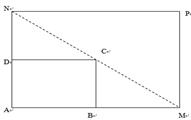
(Ⅰ)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(Ⅱ)当DN 的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值。
已知函数 是定义在R上的单调函数,满足
是定义在R上的单调函数,满足 ,且对任意的实数
,且对任意的实数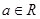 有
有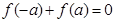 恒成立
恒成立
(Ⅰ)试判断 在R上的单调性,并说明理由.
在R上的单调性,并说明理由.
(Ⅱ)解关于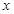 的不等式
的不等式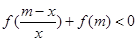 ,其中
,其中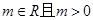
.已知函数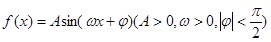 的图像与y轴的交点为
的图像与y轴的交点为 他在y轴右侧的第一个最高点和第一个最低点的坐标分别为
他在y轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和 。
。
(Ⅰ)求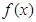 的解析式及
的解析式及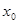 值;
值;
(Ⅱ)若锐角 满足
满足 ,求
,求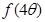 的值
的值
14分)已知函数
(1)当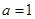 时,求函数
时,求函数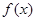 的最值;
的最值;
(2)求函数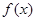 的
的 单调
单调 区间;
区间;
(3)说明是否存在实数 使
使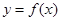 的图象与
的图象与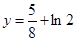 无公共点.
无公共点.
( 12分)如图,椭圆的方程为 ,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上
,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上 半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5
半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5 .
.
(1)求椭圆的方程;
(2)设直线l过F点(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.