(本题满分14分)若定义在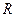 上的函数
上的函数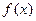 同时满足下列三个条件:
同时满足下列三个条件:
①对任意实数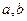 均有
均有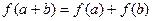 成立;
成立;
②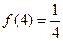
③当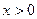 时,都有
时,都有 成立。
成立。
(1)求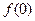 ,
,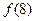 的值;
的值;
(2)求证: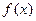 为
为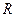 上的增函数
上的增函数
(3)求解关于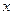 的不等式
的不等式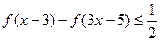 .
.
已知圆 以原点为圆心,且与圆
以原点为圆心,且与圆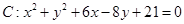 外切.
外切.
(1)求圆 的方程;
的方程;
(2)求直线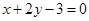 与圆
与圆 相交所截得的弦长.
相交所截得的弦长.
已知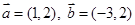 .
.
(1)求 的值
的值
(2)若 与
与 垂直,求实数
垂直,求实数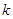 的值.
的值.
已知 ,求下列各式的值:
,求下列各式的值:
(1) ;
;
(2) .
.
已知函数f(x)=x-xlnx , ,其中
,其中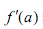 表示函数f(x)在
表示函数f(x)在
x=a处的导数,a为正常数.
(1)求g(x)的单调区间;
(2)对任意的正实数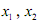 ,且
,且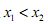 ,证明:
,证明:
(3)对任意的
如图6,已知动圆M过定点F(1,0)且与x轴相切,点F 关于圆心M 的对称点为 F',动点F’的轨迹为C.
(1)求曲线C的方程;
(2)设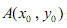 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.
①证明:直线PQ的斜率为定值;
②记曲线C位于P 、Q两点之间的那一段为l.若点B在l上,且点B到直线PQ的
距离最大,求点B的坐标.