(本小题满分14分)设函数 ,
,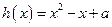 .
.
(Ⅰ)当 时,
时,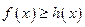 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)当 时,若函数
时,若函数 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 的取值
的取值 范围;
范围;
(Ⅲ)是否存在实数 ,使函数
,使函数 和函数
和函数 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知函数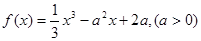
(1)求函数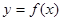 的单调区间;
的单调区间;
(2)若在区间[0,2]上恒有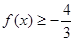 ,求
,求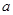 的取值范围.
的取值范围.
已知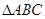 中,
中,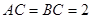 ,
,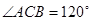 ,
,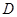 为
为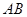 的中点,
的中点,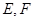 分别在线段
分别在线段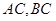 上,且
上,且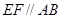
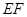 交
交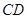 于
于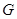 ,把
,把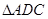 沿
沿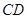 折起,如下图所示,
折起,如下图所示,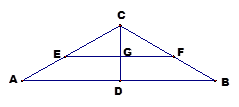
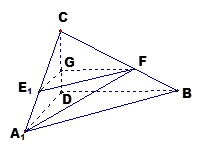
(1)求证: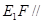 平面
平面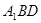 ;
;
(2)当二面角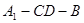 为直二面角时,是否存在点
为直二面角时,是否存在点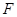 ,使得直线
,使得直线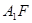 与平面
与平面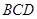 所成的角为
所成的角为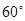 ,若存在求
,若存在求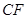 的长,若不存在说明理由.
的长,若不存在说明理由.
已知等比数列 中,
中, 且
且 ,
, ,
, 成等差数列,
成等差数列,
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项的和.
项的和.
已知 ,其中
,其中
(1)求函数 的最小正周期,并从下列的变换中选择一组合适变换的序号,经过这组变换的排序,可以把函数
的最小正周期,并从下列的变换中选择一组合适变换的序号,经过这组变换的排序,可以把函数 的图像变成
的图像变成 的图像;(要求变换的先后顺序)
的图像;(要求变换的先后顺序)
①纵坐标不变,横坐标变为原来的 倍,
倍,
②纵坐标不变,横坐标变为原来的2倍,
③横坐标不变,纵坐标变为原来的 倍,
倍,
④横坐标不变,纵坐标变为原来的 倍,
倍,
⑤向上平移一个单位,
⑥向下平移一个单位,
⑦向左平移 个单位,
个单位,
⑧向右平移 个单位,
个单位,
⑨向左平移 个单位,
个单位,
⑩向右平移 个单位,
个单位,
(2)在 中角
中角 对应边分别为
对应边分别为 ,
,

 ,求
,求 的长.
的长.
已知 (
(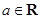 ).
).
(1)当 时,判断
时,判断 在定义域上的单调性;
在定义域上的单调性;
(2)若 在
在 上的最小值为
上的最小值为 ,求
,求 的值;
的值;
(3)若 在
在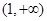 上恒成立,试求
上恒成立,试求 的取值范围.
的取值范围.