计算: (1)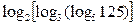 (2)
(2)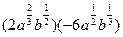 ÷
÷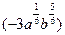
(3)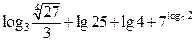
已知函数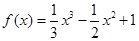 ,
,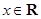 .
.
(1)求函数 的极大值和极小值;
的极大值和极小值;
(2)求函数图象经过点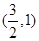 的切线的方程;
的切线的方程;
(3)求函数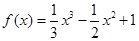 的图象与直线
的图象与直线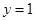 所围成的封闭图形的面积.
所围成的封闭图形的面积.
已知定义域为R的函数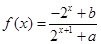 是奇函数.
是奇函数.
(1)求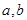 的值;
的值;
(2)若对任意的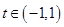 ,不等式
,不等式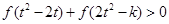 恒成立,求
恒成立,求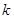 的取值范围.
的取值范围.
设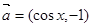 ,
,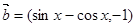 ,函数
,函数
(1)用五点作图法画出函数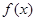 在一个周期上的图象;
在一个周期上的图象;
(2)求函数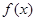 的单调递减区间和对称中心的坐标;
的单调递减区间和对称中心的坐标;
(3)求不等式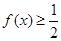 的解集; (4)如何由
的解集; (4)如何由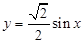 的图象变换得到
的图象变换得到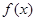 的图象.
的图象.
(本小题共13分)已知数列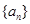 的前
的前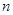 项和
项和 满足
满足 ,
, ,
, .
.
(Ⅰ)如果 ,求数列
,求数列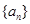 的通项公式;
的通项公式;
(Ⅱ)如果 ,求证:数列
,求证:数列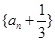 为等比数列,并求
为等比数列,并求 ;
;
(Ⅲ)如果数列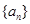 为递增数列,求
为递增数列,求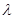 的取值范围.
的取值范围.
(本小题共14分)在平面直角坐标系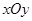 中,椭圆
中,椭圆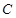 :
: 的一个顶点为
的一个顶点为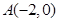 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆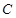 的标准方程;
的标准方程;
(Ⅱ)直线 过点
过点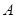 ,过
,过 作
作 的平行线交椭圆
的平行线交椭圆 于P,Q两点,如果以PQ为直径的圆与直线
于P,Q两点,如果以PQ为直径的圆与直线 相切,求
相切,求 的方程.
的方程.