某中学 的高二(1)班男同学有
的高二(1)班男同学有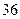 名,女同学有
名,女同学有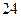 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个 人的课外兴趣小组.
人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(3)试验结束后,第一次做试验的甲同学得到的试验数据为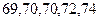 ,第二次做试验的乙同学得
,第二次做试验的乙同学得 到的试验数据为
到的试验数据为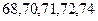 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.
已知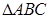 中,角A,B,C,所对的边分别是
中,角A,B,C,所对的边分别是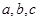 ,且
,且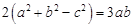 ;
;
(1)求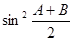
(2)若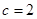 ,求
,求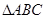 面积的最大值.
面积的最大值.
(本小题12分)已知点A(0,-2),椭圆E: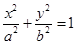 (a>b>0)的离心率为
(a>b>0)的离心率为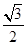 ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为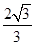 ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;(2)设过点A的动直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.
(本小题12分)在平面直角坐标系 中,点
中,点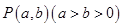 为动点,
为动点,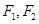 分别为椭圆
分别为椭圆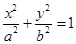 (a>b>0)的左右焦点.已知△
(a>b>0)的左右焦点.已知△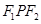 为等腰三角形.
为等腰三角形.
(Ⅰ)求椭圆的离心率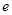 ;
;
(Ⅱ)设直线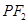 与椭圆相交于
与椭圆相交于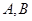 两点,
两点,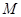 是直线
是直线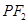 上的点,满足
上的点,满足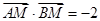 ,求点
,求点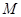 的轨迹方程.
的轨迹方程.
(本小题12分)如图,设P是圆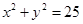 上的动点,点D是P在x轴上的射影,M为PD上一点,且
上的动点,点D是P在x轴上的射影,M为PD上一点,且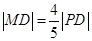
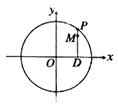
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为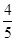 的直线被C所截线段的长度
的直线被C所截线段的长度
(本小题12分)已知F1,F2分别是椭圆 (a>b>0)的左、右焦点,A是椭圆上位于第一象限内的一点,
(a>b>0)的左、右焦点,A是椭圆上位于第一象限内的一点, =0,若椭圆的离心率等于
=0,若椭圆的离心率等于 .
.
(1)求直线AO的方程(O为坐标原点);
(2)直线AO交椭圆于点B,若△ABF2的面积等于 ,求椭圆的方程.
,求椭圆的方程.