命题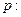 方程
方程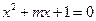 有两个不等的正实数根,命题
有两个不等的正实数根,命题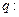 方程
方程 无实数根。若“
无实数根。若“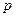 或
或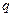 ”为真命题,求
”为真命题,求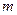 的取值范围。
的取值范围。
已知函数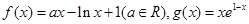 。
。
(1)求函数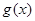 在区间
在区间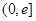 上的值域;
上的值域;
(2)是否存在实数a,对任意给定的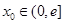 ,在区间
,在区间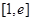 上都存在两个不同的
上都存在两个不同的 ,使得
,使得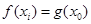 成立.若存在,求出a的取值范围;若不存在,请说明理由.
成立.若存在,求出a的取值范围;若不存在,请说明理由.
在数列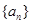 中,
中,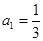 ,且前n项的算术平均数等于第n项的
,且前n项的算术平均数等于第n项的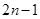 倍(
倍(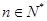 ).
).
(1)写出此数列的前5项;
(2)归纳猜想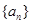 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落,小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中。已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是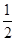 .
.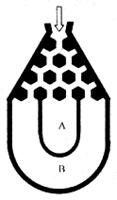
(1)求小球落入A袋中的概率P(A);
(2)在容器入口处依次放入4个小球,记X为落入A袋中小球的个数,试求X=3的概率和X的数学期望EX.
已知 是二次函数,方程
是二次函数,方程 有两个相等的实数根,且
有两个相等的实数根,且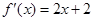 。
。
(1)求 的表达式;
的表达式;
(2)若直线 把
把 的图象与两坐标轴围成的图形面积二等分,求t的值.
的图象与两坐标轴围成的图形面积二等分,求t的值.
已知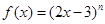 展开式的二项式系数和为512,且
展开式的二项式系数和为512,且
 .
.
求 的值;(2)求
的值;(2)求 的值.
的值.