(本小题满分12分)设数列{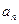 }满足
}满足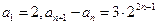 。
。
(1)求数列{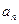 }的通项公式;
}的通项公式;
(2)令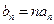 ,求数列{
,求数列{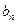 }的前n项和
}的前n项和 。
。
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,EC=ED.
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点.若CF∥AB,证明:
(1)CD=BC;
(2)△BCD∽△GBD.
如图,AB是圆O的直径,D,E为圆O上位于AB异侧的两点,连结BD并延长至点C,使BD=DC,连结AC,AE,DE.
求证:∠E=∠C.
如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连结DB并延长交⊙O于点E.证明:
(1)AC·BD=AD·AB;
(2)AC=AE.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D。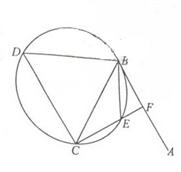
(1)证明:DB=DC;
(2)设圆的半径为1,BC=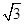 ,延长CE交AB于点F,求△BCF外接圆的半径。
,延长CE交AB于点F,求△BCF外接圆的半径。