已知x>0, y>0, 且x+y="1," 求 的最小值。
的最小值。
已知集合A={a,b,c},其中a,b,c是三个连续的自然数。如果a,b,c能够作为一个三角形的三边长,且该三角形的最大角是最小角的2倍,求所有满足条件的集合A。
(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出商品件数与商品单价的降低值x (单位:元,0≤x≤30)的平方成正比,已知商品单价降低2元时,一星期多卖出24件。
(1)将一个星期的商品销售利润表示成x的函数 ;
;
(2)如何定价才能使一个星期的商品销售利润最大?
数列{an}是等差数列, ,
, ,
, ,其中
,其中 ,数列{an}前n项和存在最小值。
,数列{an}前n项和存在最小值。
(1)求通项公式an
(2)若 ,求数列
,求数列 的前n项和
的前n项和
已知向量 ,
, ,
,
(1)求函数 最小正周期;
最小正周期;
(2)当 ,求函数
,求函数 的最大值及取得最大值时的
的最大值及取得最大值时的 ;
;
(本小题满分10分)
如图,在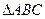 中,
中, ,BE是
,BE是 角平分线,
角平分线,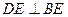 交AB于D,
交AB于D, 是
是 的外接圆。
的外接圆。
(1)求证:AC是 的切线;(2)如果AD=6,AE=
的切线;(2)如果AD=6,AE= ,求BC的长。
,求BC的长。