某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40
元.厂方在开展促销活动期间，向客户提供两种优惠方案：
① 买一套西装送一条领带；
② 西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套，领带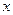
条(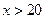
).
（1）若该客户按方案①购买，需付款 元（用含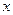的代数式表示）;
若该客户按方案②购买，需付款 元（用含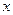的代数式表示）.
（2）若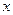=30，通过计算说明此时按哪种方案购买较为合算？
如图，山上有一座铁塔，山脚下有一矩形建筑物ABCD，且建筑物周围没有开阔平整地带．该建筑物顶端宽度AD和高度DC都可直接测得，从A、D、C三点可看到塔顶端H．可供使用的测量工具有皮尺、测角仪．
（1）请你根据现有条件，充分利用矩形建筑物，设计一个测量塔顶端到地面高度HG的方案．具体要求如下：①测量数据尽可能少；②在所给图形上，画出你设计的测量平面图，并将应测数据标记在图形上（如果测A、D间距离，用m表示；如果测D、C间距离，用n表示；如果测角，用α、β、γ表示）；
（2）根据你测量的数据，计算塔顶端到地面的高度HG（用字母表示，测角仪高度忽略不计）．
（贵州六盘水）为践行党的群众路线，六盘水市教育局开展了大量的教育教学实践活动．下图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形．
活动中测得数据如下：
①小明的身高DC＝1.5m；
②小明的影长CE＝1.7m；
③小明的脚到旗杆底部的距离BC＝9m；
④旗杆的影长BF＝7.6m；
⑤从D点看A点的仰角为30°．
请选择你需要的数据，求出旗杆的高度．（计算结果精确到0.1，参考数据：
，
）
某校九(1)班的同学在上学期的社会实践活动中，对学校旁边的山坡护墙和旗杆进行了测量．
(1)如图①，第一小组用一根木条CD斜靠在护墙上，使得DB与CB的长度相等，如果测量得到∠CDB＝38°，求α的度数．
(2)如图②，第二小组用皮尺量得EF的长为16米(E为护墙上的端点)，EF的中点距离地面FB的高度为1.9米，请你求出E点距离地面FB的高度．
(3)如图③，第三小组利用第一、第二小组的结果，来测量护墙上旗杆的高度，在点P处测得旗杆顶端A的仰角为45°，向前走4米到达点Q处，测得A的仰角为60°，求旗杆的高度AE(精确到0.1米．参考数据：tan60°≈1.732，tan30°≈0.577，
，
)．
如图，某翼装飞行员自距离水平地面500m的A处出发，沿着俯角为15°的方向，直线滑行1600m到达D点处，然后打开降落伞以75°的俯角降落到地面上的B点处．求他飞行的水平距离BC．(结果精确到1m)
如图，某学校新建了一座吴玉章雕塑，小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°，看雕塑底部C的仰角为30％，求雕塑的高度CD．(最后结果精确到0.1米，参考数据：
)