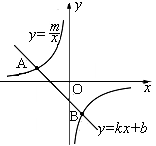(本题10分)如图,在Rt△ABC中,∠B=90°,AB=1,BC=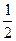 ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
(1)求AE的长度;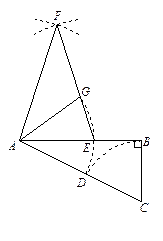
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,
①求证:△AEG∽△FEA;
②试猜想∠EAG的大小,并说明理由.
如图,这是某市部分简图,请建立适当的平面直角坐标系,分别写出各地的坐标。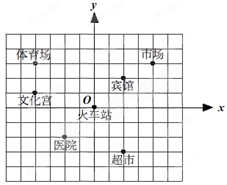
(本题14分)如图,已知正比例函数和反比例函数的图象都经过点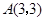 .
.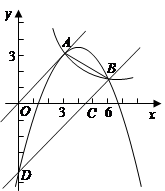
(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点 ,求
,求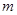 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与 轴、
轴、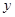 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
(4)在第(3)问的条件下,二次函数的图象上是否存在点E,使 的面积
的面积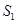 与
与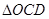 的面积S满足:
的面积S满足: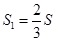 ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.
(本题12分)某商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件.设这种商品的销售单价为x元,商品每天销售这种商品所获得的利润为y元.
(1)给定x的一些值,请计算y的一些值.
| x |
… |
7 |
8 |
9 |
10 |
11 |
… |
| y |
… |
… |
(2)求y与x之间的函数关系式,并探索:当商品的销售单价定为多少元时,该商店销售这种商品获得的利润最大?这时每天销售的商品是多少件?
(本题12分)如图二次函数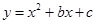 的图象经过
的图象经过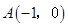 和
和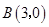 两点,
两点,
且交 轴于点
轴于点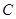 .
.
(1)试确定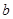 、
、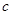 的值;
的值;
(2)过点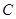 作
作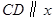 轴交抛物线于点D,点
轴交抛物线于点D,点 为此抛物线的顶点,试确定
为此抛物线的顶点,试确定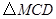 的形状.
的形状.
(本题12分)如图,已知点A(-4,2)、B(n,-4)是一次函数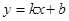 的图象与反比例函数
的图象与反比例函数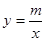 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数的解析式和点B的坐标;
(2)根据图象写出使一次函数的值小于反比例函数值的x的取值范围.