医学上为了研究传染病在传播的过程中病毒细胞的生长规律及其预防措施,将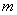 个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
| 时间(小时) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 病毒细胞总数(个) |
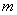 |
2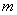 |
4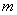 |
8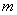 |
16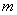 |
32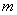 |
64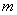 |
已知该种病毒细胞在小白鼠体内超过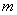
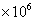 个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.
个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.
(1)在16小时内,写出病毒细胞的总数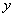 与时间
与时间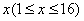 的函数关系式;
的函数关系式;
(2)为了使小白鼠在实验过程中不死亡,最迟应在何时注射该种药物.(精确到整数,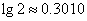 )
)
如图,在四棱锥P-ABCD中,PA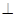 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(Ⅰ)试证:CD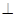 平面BEF;
平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于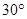 ,求k的取值范围.
,求k的取值范围.
等差数列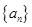 的首项为
的首项为 ,公差
,公差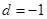 ,前
,前 项和为
项和为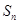 ,其中
,其中 .
.
(Ⅰ)若存在 ,使
,使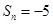 成立,求
成立,求 的值;
的值;
(Ⅱ)是否存在 ,使
,使 对任意大于1的正整数
对任意大于1的正整数 均成立?若存在,求出
均成立?若存在,求出 的值;否则,说明理由.
的值;否则,说明理由.
已知向量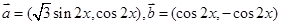 .
.
(Ⅰ)若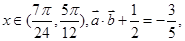 求
求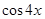 ;
;
(Ⅱ)设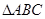 的三边
的三边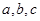 满足
满足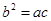 ,且边
,且边 所对应的角为
所对应的角为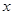 ,若关于
,若关于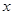 的方程
的方程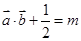 有且仅有一个实数根,求
有且仅有一个实数根,求 的值.
的值.
(本小题满分14分)
已知函数 。
。
(Ⅰ)求函数 的单调区间。
的单调区间。
(Ⅱ)若 上恒成立,求实数
上恒成立,求实数 的取值范围
的取值范围
(Ⅲ)在(Ⅱ)的条件下,对任意的 ,求证:
,求证: 。
。
(本小题满分12分)
已知椭圆C: 的短轴长为
的短轴长为 ,且斜率为
,且斜率为 的直线
的直线 过椭圆C的焦点及点
过椭圆C的焦点及点 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知一直线 过椭圆C的左焦点
过椭圆C的左焦点 ,交椭圆于点P、Q,
,交椭圆于点P、Q,
(ⅰ)若满足 (
( 为坐标原点),求
为坐标原点),求 的面积;
的面积;
(ⅱ)若直线 与两坐标轴都不垂直,点M在
与两坐标轴都不垂直,点M在 轴上,且使
轴上,且使 为
为 的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。
的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。