已知直线l的倾斜角为135°,且经过点P(1,1).
(Ⅰ)求直线l的方程;
(Ⅱ)求点A(3,4)关于直线l的对称点A¢的坐标.
(本小题满分10分)
已知向量 ,
, ,
,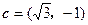 ,其中
,其中 .
.
(Ⅰ)当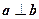 时,求
时,求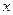 值的集合; (Ⅱ)求
值的集合; (Ⅱ)求 的最大值.
的最大值.
(本小题满分10分)
已知
(Ⅰ)若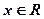 ,求f(x)的单调增区间;
,求f(x)的单调增区间;
(Ⅱ)若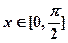 时,f(x)的最大值为4,求a的值.
时,f(x)的最大值为4,求a的值.
(本小题满分10分)
已知函数f ( x ) = ( a > 0且a ≠1)图象经过点Q(8, 6).
( a > 0且a ≠1)图象经过点Q(8, 6).
(Ⅰ) 求a的值,并在直角坐标系中画出函数f ( x )的大致图象;
(Ⅱ) 求函数f ( t ) – 9的零点.
(本小题满分10分)
以下是计算 程序框图。
程序框图。
(Ⅰ)请补上缺漏的部分①②③
(Ⅱ)请写出对应的程序.
已知函数 ,
,
(1)设两曲线 与
与 有公共点,且在公共点处的切线相同,若
有公共点,且在公共点处的切线相同,若 ,试建立
,试建立 关于
关于 的函数关系式,并求
的函数关系式,并求 的最大值;
的最大值;
(2)若 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求 的取值范围.
的取值范围.