（本题8分）
某数学兴趣小组，利用树影测量树高．已测出树AB的影长AC为9米，并测出此时太阳光线与地面成30°夹角．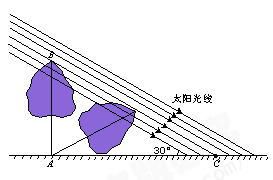 
（1）求出树高AB；
（2）因水土流失，此时树AB沿太阳光线方向倒下，在倾倒过程中，树影长度发生了变化，假设太阳光线与地面夹角保持不变。①求树与地面成45°角时的影长。
②试求树影的最大长度．
（计算结果精确到0.1米，参考数据：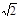
≈1.414， 
≈1.732）
（本题满分12分，第（1）题7分，第（2）题5分）
如图，在⊙O中，直径AB与弦CD垂直，垂
足为E，连接AC，将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．
（1）证明：直线FC与⊙O相切；
（2）若
，求证：四边形OCBD是菱形．
（本题满分10分，第（1）小题4分，第（2）小题6分）
如图，正方形ABCD中， M是边BC上一点，且BM
=
.
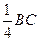（1）若
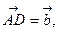试用
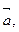
表示
；
（2）若AB=4
|
|
，求sin∠AMD的值.
已知：在矩形AOBC中，OB＝4，OA＝3，分别以OB、OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系，F是边BC上的一个动点（不与B、C重合），过F点的反比例函数
（k＞0）的图象与AC边交于点E.
（1）求证：△AOE与△BOF的面积相等.
（2）记S＝S△OEF－S△ECF，求当k为何值时，S有最大值，最大值为多少？
（3）请探索：是否存在这样的点F，使得将△CEF沿EF对折后，C点恰好落在OB上？若存
在，请直接写出点F的坐标，若不存在，请说明理由.
将一副三角尺如图拼接：含30°角的三角尺（△ABC）的长直角边与含45°角的三角尺（△ACD）的斜边恰好重合．已知AB＝2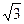
，P是线段AC上的一个动点．
（1）当点P运动到∠ABC的平分线上时，连结DP，求DP的长；
（2）当点P在运动过程中出现PD＝BC时，∠PDA=；
（3）当PC=时，以D，P，B，Q为顶点的平行四边形的顶点Q恰好在边BC上，
此时□DPBQ的面积=．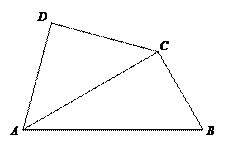
某家庭装修房屋，先由甲装修公司单独装修3天，剩下的工作由甲、乙
两个装修公司合作完成.工程进度满足如图所示的函数关系，该家庭共支付工资8000元.
（1）求合作部分工作量y与工作时间x之间的函数关系式；
（2）完成此房屋装修共需多少天？
（3）若按完成工作量的多少支付工资，甲装修公司应得多少元？
