(本小题满分14分)
已知二次函数 满足:
满足: ,
,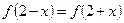 ,且该函数的最小值为1.
,且该函数的最小值为1.
⑴ 求此二次函数 的解析式;
的解析式;
⑵ 若函数 的定义域为
的定义域为 =
=  .(其中
.(其中 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数 的值域也为
的值域也为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设命题p:函数 在(0,+
在(0,+ )上是增函数;命题q:方程
)上是增函数;命题q:方程 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。
(1)求点P(a,b)的轨迹图形的面积;
(2)求a+5b的取值范围。
某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定对这种食品生产厂家提供政府补贴,设这种食品的市场价格为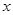 元/千克,政府补贴为
元/千克,政府补贴为 元/千克,根据市场调查,当
元/千克,根据市场调查,当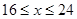 时,这种食品市场日供应量
时,这种食品市场日供应量 万千克与市场日需量
万千克与市场日需量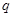 万千克近似地满足关系:
万千克近似地满足关系: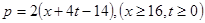 ,
, 。当
。当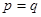 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。
(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域;
(2)为使市场平衡价格不高于每千克20元,政府补贴至少为每千克多少元?
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成直二面角 ,如图二,在二面角
,如图二,在二面角 中.
中.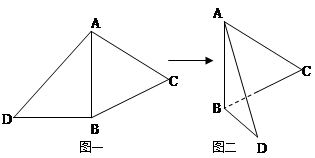
(1)求证:BD⊥AC;
(2)求D、C之间的距离;
(3)求DC与面ABD成的角的正弦值。
设函数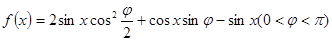 在
在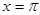 处取最小值.
处取最小值.
(1)求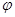 的值;
的值;
(2)在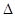 ABC中,
ABC中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知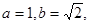
 ,求值
,求值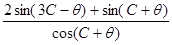 .
.
已知函数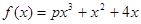 (常数
(常数 )在
)在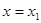 处取得极大值M.
处取得极大值M.
(Ⅰ)当M=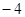 时,求
时,求 的值;
的值;
(Ⅱ)记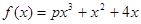 在
在 上的最小值为N,若
上的最小值为N,若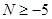 ,求
,求 的取值范围.
的取值范围.