(本小题满分12分)为了了解2011年某校高三学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为(3.9,4.2],(4.2,4.5],… ,(5.1,5.4].经过数据处理,得到如下频率分布表:
| 分组 |
频数 |
频率 |
| (3.9,4.2] |
3 |
0.06 |
| (4.2,4.5] |
6 |
0.12 |
| (4.5,4.8] |
25 |
x |
| (4.8,5.1] |
y |
z |
| (5.1,5.4] |
2 |
0.04 |
| 合计 |
n |
1.00 |
(I)求频率分布表中未知量n,x,y,z的值;
(II)从样本中视力在(3.9,4.2]和(5.1,5.4]的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
已知集合A=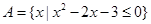 ,
,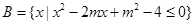
(1)若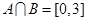 ,求实数
,求实数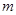 的值;
的值;
(2)若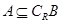 ,求实数
,求实数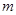 的取值范围.
的取值范围.
(本小题满分14分)设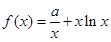 ,
,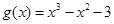 .
.
(1)当 时,求曲线
时,求曲线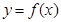 在
在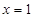 处的切线方程;
处的切线方程;
(2)如果存在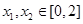 ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数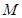 ;
;
(3)如果对任意的 ,都有
,都有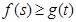 成立,求实数
成立,求实数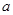 的取值范围.
的取值范围.
(本小题满分13分)已知几何体A—BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)试探究在DE上是否存在点Q,使得AQ BQ并说明理由.
BQ并说明理由.
(本小题满分12分)首届世界低碳经济大会11月17日在南昌召开,本届大会以“节能减排,绿色生态”为主题。某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
(本小题满分12分)设数列 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 ,
, .
.
(Ⅰ) 求数列 的通项公式;
的通项公式;
(Ⅱ) 若 ,
, 为数列
为数列 的前
的前 项和. 求证:
项和. 求证: .
.