(本小题满分12分)口袋里有分别标有数字1、2、3、4的4只白球和分别标有数字5、6的2只红球,这些球除了颜色和所标数字外完全相同.某人从中随机取出一球,记下球上所标数字后放回,再随机取出一球并记下球上所标数字,
(Ⅰ)求两次取出的球上的数字之和大于8的概率;
(Ⅱ)求两次取出的球颜色不同的概率;
(本小题满分14分)已知函数 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(Ⅰ)判断函数 在
在 内的零点的个数,并说明理由;
内的零点的个数,并说明理由;
(Ⅱ)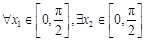 ,使得不等式
,使得不等式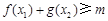 成立,试求实数
成立,试求实数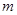 的取值范围;
的取值范围;
(Ⅲ)若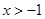 ,求证:
,求证: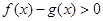 .
.
(本小题满分12分)已知抛物线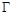 的顶点为坐标原点,焦点为
的顶点为坐标原点,焦点为 .
.
(Ⅰ)求抛物线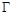 的方程;
的方程;
(Ⅱ)若点 为抛物线
为抛物线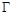 的准线上的任意一点,过点
的准线上的任意一点,过点 作抛物线
作抛物线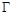 的切线
的切线 与
与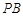 ,切点分别为
,切点分别为 ,求证:直线
,求证:直线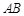 恒过某一定点;
恒过某一定点;
(Ⅲ)分析(Ⅱ)的条件和结论,反思其解题过程,再对命题(Ⅱ)进行变式和推广.请写出一个你发现的真命题,不要求证明(说明:本小题将根据所给出的命题的正确性和一般性酌情给分).
(本小题满分12分)一种药在病人血液中的含量不低于2克时,它才能起到有效治疗的作用.已知每服用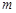 (
(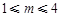 且
且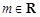 )个单位的药剂,药剂在血液中的含量
)个单位的药剂,药剂在血液中的含量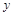 (克)随着时间
(克)随着时间 (小时)变化的函数关系式近似为
(小时)变化的函数关系式近似为 ,其中
,其中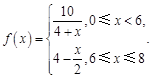
(Ⅰ)若病人一次服用3个单位的药剂,则有效治疗时间可达多少小时?
(Ⅱ)若病人第一次服用2个单位的药剂,6个小时后再服用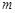 个单位的药剂,要使接下来的2小时中能够持续有效治疗,试求
个单位的药剂,要使接下来的2小时中能够持续有效治疗,试求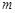 的最小值.
的最小值.
(本小题满分12分)已知函数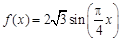 在同一半周期内的图象过点
在同一半周期内的图象过点 ,其中
,其中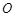 为坐标原点,
为坐标原点, 为函数
为函数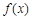 图象的最高点,
图象的最高点,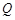 为函数
为函数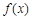 的图象与
的图象与 轴的正半轴的交点.
轴的正半轴的交点.
(Ⅰ)试判断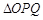 的形状,并说明理由.
的形状,并说明理由.
(Ⅱ)若将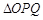 绕原点
绕原点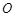 按逆时针方向旋转角
按逆时针方向旋转角 时,顶点
时,顶点 恰好同时落在曲线
恰好同时落在曲线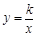
 上(如图所示),求实数
上(如图所示),求实数 的值.
的值.
(本小题满分12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某被邀请者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(Ⅱ)假定(Ⅰ)中被邀请到的3个人中恰有两人接受挑战.根据活动规定,现记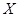 为接下来被邀请到的6个人中接受挑战的人数,求
为接下来被邀请到的6个人中接受挑战的人数,求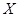 的分布列和均值(数学期望).
的分布列和均值(数学期望).