已知直角梯形ABCD中, ,
,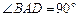 ,且
,且 ,点E、F分别在AD、BC上,满足
,点E、F分别在AD、BC上,满足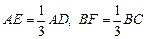 .现将此梯形沿EF折叠成如图所示图形,且使
.现将此梯形沿EF折叠成如图所示图形,且使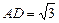 .
.
(1)求证:AE⊥平面ABCD;
(2)求二面角 的大小.
的大小.
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列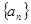 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列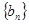 的前六项.(Ⅰ)求等比数列
的前六项.(Ⅰ)求等比数列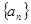 的通项公式;
的通项公式;
(Ⅱ)求等差数列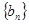 的通项公式;(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率
的通项公式;(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率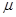 的大小.
的大小.
(本小题满分12分)如图,圆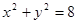 内有一点P(—1,2),AB为过点P的弦。
内有一点P(—1,2),AB为过点P的弦。
(1)当弦AB的倾斜角为135°时,求AB所在的直线方程及|AB|;
(2)当弦AB被点P平分时,写出直线AB的方程。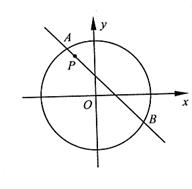
设不等式组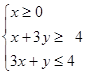 表示的平面区域为D。
表示的平面区域为D。
(1)在直角坐标系中画出平面区域D
(2)若直线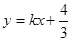 分平面区域D为面积相等的两部分,求k得值。
分平面区域D为面积相等的两部分,求k得值。
国家射击队的队员为在2010年亚运会上取得优异成绩,正在加紧备战,经过近期训练,某队员射击一次,命中7~10环的概率如下表所示:
| 命中环数 |
10环 |
9环 |
8环 |
7环 |
| 概率 |
0.32 |
0.28 |
0.18 |
0.12 |
求该射击队员射击一次
(1)射中9环或10环的概率;
(2)至少命中8环的概率;
(3)命中不足8环的概率.
已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.试确定m、n的值,分别使
(1)l1与l2相交于点P(m,-1);
(2)l1∥l2;
(3)l1⊥l2且l1在y轴上的截距为-1.