某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),年
产量不足80千件时,C(x)= 2+10x(万元);当年产量不小于80千件时,
2+10x(万元);当年产量不小于80千件时,
C(x)=51x+ -1450(万元).通过市场分析,若每件售价为500元时,该厂当年生产
-1450(万元).通过市场分析,若每件售价为500元时,该厂当年生产
的该产品能全部销售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一产品的生产中所获利润最大,最大利润是多少?
设数列{an}的前n项和为Sn,且Sn=(m+1)-man 对任意正整数n都成立,其中m为常数,且m<-1.
对任意正整数n都成立,其中m为常数,且m<-1.
(1)求证:{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足:b1= a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时,
a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时, 成立?
成立?
数列{an}中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*).
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn;
(3)设bn=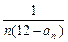 (n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m,使得对任意n∈N*均有Tn>
(n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m,使得对任意n∈N*均有Tn> 成立?若存在,求出m的值;若不存在,说明理由.
成立?若存在,求出m的值;若不存在,说明理由.
数列{an}满足a1=2,对于任意的n∈N*都有an>0,且(n+1)an2+an·an+1-nan+12=0,又知数列{bn}的通项为bn=2n-1+1.
(1)求数列{an}的通项an及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn与Tn的大小关系,并说明理由.
{an}为等差数列,公差d≠0,an≠0,(n∈N*),且akx2+2ak+1x+ak+2=0(k∈N*)
(1)求证:当k取不同自然数时,此方程有公共根;
(2)若方程不同的根依次为x1,x2,…,xn,…,
求证:数列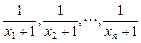 为等差数列.
为等差数列.
设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2·b4=a3,分别求出{an}及{bn}的前n项和S10及T10.