(本小题满分12分)
某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数
分布)如下表:
| 学历 |
35岁以下 |
35~50岁 |
50岁以上 |
| 本科 |
80 |
30 |
20 |
| 研究生 |
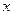 |
20 |
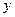 |
(1)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本
看成一个总体, 从中任取2人, 求至少有1人的学历为研究生的概率;
(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取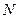 个人,其中35岁以
个人,其中35岁以
下48人,50岁以上10人,再从这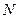 个人中随机抽取出1人,此人的年龄为50岁以上
个人中随机抽取出1人,此人的年龄为50岁以上
的概率为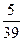 ,求
,求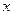 、
、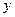 的值.
的值.
经过点 ,倾斜角为
,倾斜角为 的直线
的直线 ,与曲线
,与曲线 :
: (
( 为参数)相交于
为参数)相交于 两点.
两点.
(1)写出直线 的参数方程,并求当
的参数方程,并求当 时弦
时弦 的长;
的长;
(2)当 恰为
恰为 的中点时,求直线
的中点时,求直线 的方程;
的方程;
(3)当 时,求直线
时,求直线 的方程;
的方程;
(4)当 变化时,求弦
变化时,求弦 的中点的轨迹方程.
的中点的轨迹方程.
设 ,其中
,其中 为正整数.
为正整数.
(1)求 ,
, ,
, 的值;
的值;
(2)猜想满足不等式 的正整数
的正整数 的范围,并用数学归纳法证明你的猜想.
的范围,并用数学归纳法证明你的猜想.
设函数

 .
.
(1)当 时,解关于
时,解关于 的不等式
的不等式 ;
;
(2)如果 ,
, ,求
,求 的取值范围.
的取值范围.
已知圆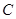 经过点
经过点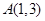 、
、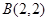 ,并且直线
,并且直线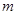 :
: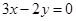 平分圆
平分圆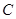 .
.
(Ⅰ)求圆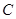 的方程;
的方程;
(Ⅱ)若过点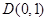 ,且斜率为
,且斜率为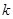 的直线
的直线 与圆
与圆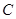 有两个不同的交点
有两个不同的交点 .
.
(ⅰ)求实数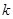 的取值范围;
的取值范围;
(ⅱ)若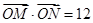 ,求
,求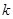 的值.
的值.
设两个向量 、
、 ,满足
,满足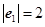 ,
,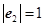 ,
, 、
、 的夹角为
的夹角为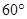 ,若向量
,若向量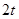
 与向量
与向量
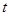
 的夹角为钝角,求实数
的夹角为钝角,求实数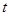 的取值范围.
的取值范围.