已知命题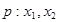 是方程
是方程 的两个实根,不等式
的两个实根,不等式 对任意实数
对任意实数 恒成立;命题
恒成立;命题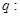 不等式
不等式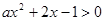 有解,若命题“
有解,若命题“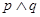 ”为假命题,“
”为假命题,“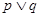 ”为真命题,求实数
”为真命题,求实数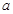 的取值范围.
的取值范围.
(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C= ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.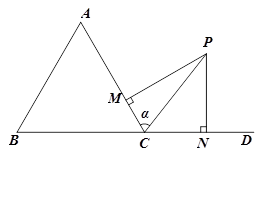
已知等比数列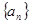 中,各项都是正数,且
中,各项都是正数,且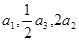 成等差数列,则
成等差数列,则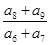 等于.
等于.
(本小题满分12分)如图,设 为抛物线
为抛物线 的焦点,
的焦点, 是抛物线上一定点,其
是抛物线上一定点,其
坐为 ,
, 为线段
为线段 的垂直平分线上一点,且点
的垂直平分线上一点,且点 到抛物线的准线
到抛物线的准线 的距离为
的距离为 .
.
(Ⅰ)求抛物线的方程;(Ⅱ)过点P任作两条斜率均存在的直线PA、PB,分别与抛物线交于点A、B,如图示,若直线AB的斜率为定值 ,求证:直线PA、PB的倾斜角互补.
,求证:直线PA、PB的倾斜角互补.
(本小题满分11分)已知函数 ,其中
,其中 ,且曲线
,且曲线 在点
在点 的
的
切线垂直于直线 .
.
(Ⅰ)求 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数 的单调区间和极值.
的单调区间和极值.
(本小题满分10分)(1)已知数列 中,
中, ,求数列
,求数列 的前
的前 项和;
项和;
(2)已知 是等比数列
是等比数列 的前
的前 项和,且公比
项和,且公比 ,
, 成等差数列,求证:
成等差数列,求证: 成等差数
成等差数
列.