( 7分)
已知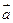 = (cosx,sinx),
= (cosx,sinx), = (-cosx,cosx),函数f (x)=
= (-cosx,cosx),函数f (x)= .
.
(Ⅰ)求函数f (x)的最小正周期;
(Ⅱ)当x∈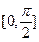 时,求f(x)的值域.
时,求f(x)的值域.
如图,已知双曲线C1: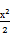 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
(1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
(3)求证:圆x2+y2= 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
已知点P是圆M:x2+(y+m)2=8(m>0,m≠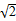 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
(1)当P在圆M上运动时,记动点Q的轨迹为曲线Г,判断曲线Г为何种曲线,并求出它的标准方程.
(2)过原点斜率为k的直线交曲线Г于A,B两点,其中A在第一象限,且它在x轴上的射影为点C,直线BC交曲线Г于另一点D,记直线AD的斜率为k′,是否存在m,使得对任意的k>0,都有|k·k′|=1?若存在,求m的值;若不存在,请说明理由.
在直角坐标系xOy中,已知圆心在第二象限、半径为2 的圆C与直线y=x相切于坐标原点O,椭圆
的圆C与直线y=x相切于坐标原点O,椭圆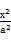 +
+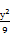 =1与圆C的一个交点到椭圆两焦点的距离之和为10.
=1与圆C的一个交点到椭圆两焦点的距离之和为10.
(1)求圆C的方程.
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段OF的长,若存在,请求出Q的坐标;若不存在,请说明理由.
已知☉M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切☉M于A,B两点.
(1)如果|AB|=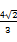 ,求直线MQ的方程.
,求直线MQ的方程.
(2)求证:直线AB恒过一个定点.
在直角坐标平面上给定一曲线y2=2x,
(1)设点A的坐标为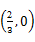 ,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
(2)设点A的坐标为(a,0),a∈R,求曲线上的点到点A距离的最小值dmin,并写出dmin=f(a)的函数表达式.