已知某养猪场每年的固定成本是20000元,每年最大规模的养殖量是400头。每养一头猪,成本增加100元。如果收入函数是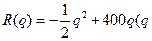 是猪的数量),每年养多少头猪可使总利润最大?总利润是多少?
是猪的数量),每年养多少头猪可使总利润最大?总利润是多少?
(本小题满分1 2分)
2分)
某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)
如下:
(I)请画出适当的统计图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩
的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答
结论). (Ⅱ)从甲、乙两人的10次成绩中各随机抽取一次,求抽取的成绩中至少有一个低
于12.8秒的概率.
(III)经过对甲、乙两位同学的若干次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]
之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率
(本小题满分l2分)
如图,在多面体ABCDEF中,ABCD为菱形, ABC=60
ABC=60 ,E
,E C
C 面ABCD,FA
面ABCD,FA 面ABCD,G
面ABCD,G
为BF的中点,若EG//面ABCD
(I)求证:EG 面ABF
面ABF
(Ⅱ)若AF=AB,求二面角B—EF—D的余弦值
(本小题满分12分)
已知数列{ }为公差不为零的等差数列,
}为公差不为零的等差数列, =1,各项均为正数的等比数列{
=1,各项均为正数的等比数列{ }的第1
}的第1
项、第3项、第5项分别是 、
、 、
、 .
.
(I )求数列{
)求数列{ }与{
}与{ }的通项公式;
}的通项公式;
(Ⅱ)求数列{
 }的前
}的前 项和.
项和.
已知数列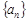 中,
中,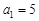 且
且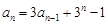 (
(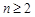 )。
)。
(1)求 ,
, 的值;
的值;
(2)设 ,是否存在实数
,是否存在实数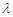 ,使数列
,使数列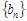 为等差数列,若存在请求其通项
为等差数列,若存在请求其通项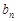 ,若不存在请说明理由。
,若不存在请说明理由。
设函数 (其中
(其中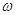 >0,
>0, ),且
),且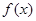 的图象在y轴右侧的第一个最高点的横坐标为
的图象在y轴右侧的第一个最高点的横坐标为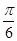 .
.
(1)求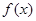 的最小正周期;
的最小正周期;
(2)如果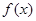 在区间
在区间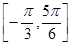 上的最小值为
上的最小值为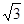 ,求a的值.
,求a的值.