(本题满分14分)
已知mÎR,设P:不等式 ;Q:函数
;Q:函数 在(-¥,+¥)上有极值.求使P正确且Q正确的m的取值范围.
在(-¥,+¥)上有极值.求使P正确且Q正确的m的取值范围.
如图,圆O的直径AB= 10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C、D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
(Ⅰ)求证: PEC=
PEC=  PDF
PDF
(Ⅱ)求PE PF的值
PF的值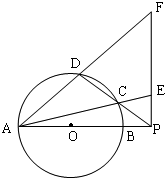
已知函数 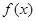 的定义域是
的定义域是 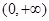 ,
, 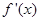 是
是 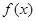 的导函数,且
的导函数,且  在
在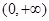 上恒成立
上恒成立
(Ⅰ)求函数 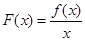 的单调区间。
的单调区间。
(Ⅱ)若函数 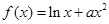 ,求实数a的取值范围
,求实数a的取值范围
(Ⅲ)设  是
是 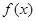 的零点 ,
的零点 ,  ,求证:
,求证:  .
.
平面内动点P(x,y)与两定点A(-2, 0), B(2,0)连线的斜率之积等于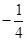 ,若点P的轨迹为曲线E,过点
,若点P的轨迹为曲线E,过点 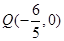 直线
直线  交曲线E于M,N两点.
交曲线E于M,N两点.
(Ⅰ)求曲线E的方程,并证明: MAN是一定值;
MAN是一定值;
(Ⅱ)若四边形AMBN的面积为S,求S的最大值
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF 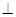 平面ABCD,BF=3,G、H分别是CE和CF的中点.
平面ABCD,BF=3,G、H分别是CE和CF的中点.
(Ⅰ)求证:AF//平面BDGH;
(Ⅱ)求 

某校学习小组开展“学生数学成绩与化学成绩的关系”的课题研究,对该校高二年级800名学生上学期期 数学和化学成绩,按优秀和不优秀分类得结果:数学和化学都优秀的有60人,数学成绩优秀但化学不优秀的有140人,化学成绩优秀但数学不优秀的有100人.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
| 数学优秀 |
数学不优秀 |
总计 |
|
| 化学优秀 |
|||
| 化学不优秀 |
|||
| 总计 |
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。