某校学习小组开展“学生数学成绩与化学成绩的关系”的课题研究,对该校高二年级800名学生上学期期 数学和化学成绩,按优秀和不优秀分类得结果:数学和化学都优秀的有60人,数学成绩优秀但化学不优秀的有140人,化学成绩优秀但数学不优秀的有100人.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
| |
数学优秀 |
数学不优秀 |
总计 |
| 化学优秀 |
|
|
|
| 化学不优秀 |
|
|
|
| 总计 |
|
|
|
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
已知四棱锥P-ABCD的直观图(如图(1))及左视图(如图(2)),底面ABCD是边长为2的正方形,平面PAB⊥平面ABCD,PA=PB。
(1)求证:AD⊥PB;
(2)求异面直线PD与AB所成角的余弦值;
(3)求平面PAB与平面PCD所成锐二面角的大小.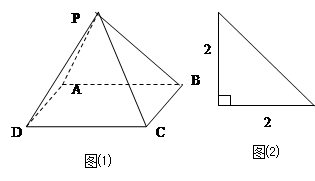
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为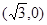
(1)求双曲线C的方程;
(2)若直线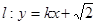 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 (其中O为原点). 求k的取值范围.
(其中O为原点). 求k的取值范围.
如图,矩形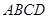 中,
中, ,
,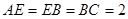 ,
, 为
为 上的点,且
上的点,且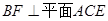 ,AC、BD交于点G.
,AC、BD交于点G.
(1)求证: ;
;
(2)求证;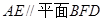 ;
;
(3)求三棱锥 的体积.
的体积.
已知命题p:“ ”,
”,
命题q:“ ”若命题“p且q”是真命题,求实数a的取值范围.
”若命题“p且q”是真命题,求实数a的取值范围.
已知集合 ,集合
,集合 ,集合
,集合
(1)求从集合 中任取一个元素是
中任取一个元素是 的概率;
的概率;
(2)从集合 中任取一个元素,求
中任取一个元素,求 的概率;
的概率;
(3)设 为随机变量,
为随机变量, ,写出
,写出 的概率分布,并求
的概率分布,并求