已知数列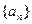 的前n项和为
的前n项和为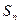 ,且
,且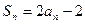 ,(n=1,2,3…)数列
,(n=1,2,3…)数列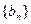 中,
中, ,点
,点 在直线
在直线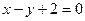 上。
上。
(Ⅰ)求数列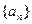 和
和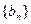 的通项公式;
的通项公式;
(Ⅱ)记 ,求满足
,求满足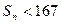 的最大正整数n。
的最大正整数n。
(本题满分15分 )已知函数 .
.
(1)求函数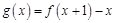 的最大值;
的最大值;
(2)若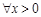 ,不等式
,不等式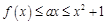 恒成立,求实数
恒成立,求实数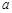 的取值范围;
的取值范围;
(3)若 ,求证:
,求证: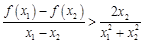 .
.
(本题满分15分 )已知椭圆
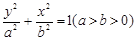 经过点
经过点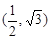 ,一个焦点是
,一个焦点是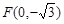 .
.
(Ⅰ)求椭圆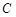 的方程;
的方程;
(Ⅱ)设椭圆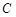 与
与 轴的两个交点为
轴的两个交点为 、
、 ,点
,点 在直线
在直线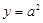 上,直线
上,直线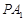 、
、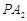 分别与椭圆
分别与椭圆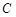 交于
交于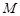 、
、 两点.试问:当点
两点.试问:当点 在直线
在直线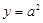 上运动时,直线
上运动时,直线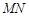 是否恒经过定点
是否恒经过定点 ?证明你的结论.
?证明你的结论.
(本题满分14分 )已知函数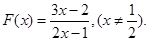
(1)求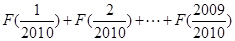 的值;
的值;
(2)已知数列 ,求证数列
,求证数列 是等差数列;
是等差数列;
(3)已知 ,求数列
,求数列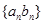 的前n项和
的前n项和 .
.
(本题满分14分 )如图,在三棱柱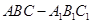 中,所有的棱长都为2,
中,所有的棱长都为2, .
.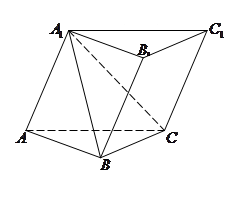
(1)求证: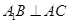 ;
;
(2)当三棱柱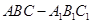 的体积最大时,
的体积最大时,
求平面 与平面
与平面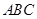 所成的锐角的余弦值.
所成的锐角的余弦值.
(本题满分14分 )在锐角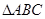 中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2
中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2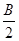 -1)=-
-1)=-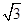 cos2B.
cos2B.
(1)求B的大小;
(2)如果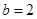 ,求
,求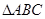 的面积
的面积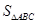 的最大值.
的最大值.