滑雪运动员不借助雪杖，从静止由山坡以加速度a1为匀加速滑下，测得20s时的速度为20m/s，50s到达坡底，又沿水平面以加速度a2匀减速滑行20s停止，求，
（1）a1和a2
（2）到达坡底后6s末的速度
竖直放置的一对平行金属板的左极板上，用长为
的轻质绝缘细线悬挂一个带电量为q质量为 m的小球，将平行金属板按如图所示的电路图连接．当滑动变阻器R在a位置时，绝缘线与左极板的夹角为θ1=30°，当将滑片缓慢地移动到b位置时，夹角为θ2=60°．两板间的距离大于，重力加速度为g．问：
（1）小球在上述两个平衡位置时，平行金属板上所带电荷量之比
（2）若保持变阻器滑片位置在a处不变，对小球再施加一个拉力，使绝缘线与竖直方向的夹角从θ1=30°缓慢地增大到θ2=60°，则此过程中拉力做的功W=？
如图所示，质量为km的斜劈，其中k>1，静止放在光滑的水平面上，斜劈的曲面光滑且为半径为R的四分之一圆面，圆面下端与光滑水平面相切。一质量为m的小球位于水平面上某位置，现给小球水平向右的初速度v0。
①若R足够大，求当小球从斜劈滑下离开时小球的速度
；
②若小球向右滑上斜劈刚好没有越过圆面上端，求k的取值 .
用折射率为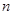
的透明物质做成内、外径分别为
、
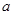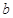的球壳，球壳的内表面涂有能完全吸收光的物质，如图所示，当一束平行光从左侧射向该球壳时，被吸收掉的光束在射进球壳左侧外表面前的横截面积有多大？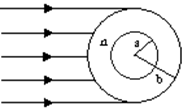
用质子流(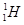
)轰击固态的重水
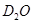，当质子和重水中的氘核(
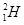)发生碰撞时，系统损失的动能如果达到核反应所需的能量，将发生生成
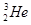核的反应。
①写出质子流轰击固态的重水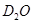的核反应方程；
②当质子具有最小动能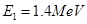
时，用质子流轰击固态的重水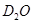（认为氘核是静止的）可发生核反应；若用氘核轰击普通水的固态冰中的质子（认为质子是静止的）时，也能发生同样的核反应，求氘核的最小动能
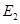。已知氘核质量等于质子质量的两倍。
如图所示，一束截面为圆形（半径R）的平行白光垂直射向一玻璃半球的平面，经折射后在屏幕S上形成一个圆形彩色亮区。已知玻璃半球的半径为R，屏幕S至球心的距离为d（d>3R），不考虑光的干涉和衍射，试问：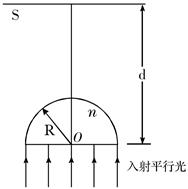
①在屏幕S上形成的圆形亮区的最外侧是什么颜色?
②若玻璃半球对最外侧色光的折射率为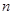
，求出圆形亮区的最大半径。