如图所示，水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘-优题课

如图所示，水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径．在轨道所在空间存在水平向右的匀强电场，电场线与轨道所在的平面平行，电场强度．现有一电荷量，质量的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体恰好能通过半圆形轨道的最高点C，然后落至水平轨道上的D点．取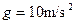．试求：
（1）带电体在圆形轨道C点的速度大小．
（2）D点到B点的距离．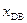
（3）带电体运动到圆形轨道B点时对圆形轨道的压力大小．
（4）带电体在从P开始运动到落至D点的过程中的最大动能．

科目物理题型计算题难度未知

如图所示，在以坐标原点 $O$ 为圆心、半径为 $R$ 的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为 $B$ ，磁场方向垂直于 $x O y$ 平面向里。一带正电的粒子（不计重力）从 $O$ 点沿 $y$ 轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经 $t_{0}$ 时间从 $p$ 点射出。
（1）求电场强度的大小和方向。

（2）若仅撤去磁场，带电粒子仍从 $O$ 点以相同的速度射入，经 $\frac{t_{0}}{2}$ 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。

（3）若仅撤去电场，带电粒子仍从 $O$ 点射入，且速度为原来的4倍，求粒子在磁场中运动的时间。

如图甲，在 $x ＜ 0$ 的空间中存在沿 $y$ 轴负方向的匀强电场和垂直于 $x o y$ 平面向里的匀强磁场，电场强度大小为 $E$ ，磁感应强度大小为 $B$ .一质量为 $q (q ＞ 0)$ 的粒子从坐标原点 $O$ 处，以初速度 $v_{0}$ 沿 $x$ 轴正方向射人，粒子的运动轨迹见图甲，不计粒子的质量。
（1）求该粒子运动到 $y = h$ 时的速度大小 $v$ ;

（2）现只改变人射粒子初速度的大小，发现初速度大小不同的粒子虽然运动轨迹（ $y - x$ 曲线）不同，但具有相同的空间周期性，如图乙所示；同时，这些粒子在 $y$ 轴方向上的运（ $y - t$ 关系）是简谐运动，且都有相同的周期 $T = \frac{2 π m}{q B}$ 。

Ⅰ 求粒子在一个周期 $T$ 内，沿 $x$ 轴方向前进的距离 $S$ ；

Ⅱ 当入射粒子的初速度大小为 $v_{0}$ 时，其 $y - t$ 图像如图丙所示，求该粒子在 $y$ 轴方向上做简谐运动的振幅 $A$ ,并写出 $y - t$ 的函数表达式。

如图为某种鱼饵自动投放器中的投饵管装置示意图，其下半部 $A B$ 是一长为 $2 R$ 的竖直细管，上半部 $B C$ 是半径为 $R$ 的四分之一圆弧弯管，管口沿水平方向， $A B$ 管内有一原长为 $R$ 、下端固定的轻质弹簧。投饵时，每次总将弹簧长度压缩到 $0.5 R$ 后锁定，在弹簧上段放置一粒鱼饵，解除锁定，弹簧可将鱼饵弹射出去。设质量为 $m$ 的鱼饵到达管口 $C$ 时，对管壁的作用力恰好为零。不计鱼饵在运动过程中的机械能损失，且锁定和解除锁定时，均不改变弹簧的弹性势能。已知重力加速度为 $g$ 。求：
（1）质量为 $m$ 的鱼饵到达管口 $C$ 时的速度大小 $v_{1}$ ;
（2）弹簧压缩到 $0.5 R$ 时的弹性势能 $E_{p}$ ;
（3）已知地面欲睡面相距 $1.5 R$ ，若使该投饵管绕 $A B$ 管的中轴线 $O O `$ 。在 $90 °$ 角的范围内来回缓慢转动，每次弹射时只放置一粒鱼饵，鱼饵的质量在 $\frac{2}{3} m$ 到 $m$ 之间变化，且均能落到水面。持续投放足够长时间后，鱼饵能够落到水面的最大面积 $S$ 是多少？

反射式调管是常用的微波器械之一，它利用电子团在电场中的震荡来产生微波，其震荡原理与下述过程类似。如图所示，在虚线 $M N$ 两侧分别存在着方向相反的两个匀强电场，一带电微粒从A点由静止开始，在电场力作用下沿直线在 $A$ 、 $B$ 两点间往返运动。已知电场强度的大小分别是 $E_{1} = 2.0 \times 10^{3} N / C$ 和 $E_{2} = 4.0 \times 10^{3} N / C$ ，方向如图所示，带电微粒质量 $m = 1.0 \times 10^{- 20} k g$ ，带电量 $q = - 1.0 \times 10^{- 9} C$ ,A点距虚线 $M N$ 的距离 $d_{1} = 1.0 c m$ ，不计带电微粒的重力，忽略相对论效应。求：
（1) $B$ 点到虚线 $M N$ 的距离 $d_{2}$ ；

（2）带电微粒从 $A$ 点运动到 $B$ 点所经历的时间 $t$ 。

如图所示，两根足够长的光滑平行金属导轨 $M N$ 、 $P Q$ 间距为 $l = 0.5 m$ ，其电阻不计，两导轨及其构成的平面均与水平面成 $30^{°}$ 角，完全相同的两金属棒 $a b$ 、 $c d$ 分别垂直导轨放置，每棒两端都与导轨始终有良好接触，已知两棒质量均为 $m = 0.02 k g$ ，电阻均为 $R = 0.1 Ω$ ，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度 $B = 0.2 T$ ，棒 $a b$ 在平行于导轨向上的力 $F$ 作用下，沿导轨向上匀速运动，而棒cd恰好能够保持静止。取 $g = 10 m / s^{2}$ ，问：

（1）通过棒 $c d$ 的电流 $I$ 是多少，方向如何？

（2）棒 $a b$ 受到的力 $F$ 多大？

（3）棒 $c d$ 每产生 $Q = 0.1 J$ 的热量，力 $F$ 做的功 $W$ 是多少？