如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,
BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点
(1)证明:直线EE1∥平面FCC1
(2)求:二面角B-FC1-C的余弦值.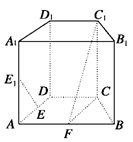
如图1-2-24所示,梯形ABCD中,AB∥CD,AB="4" cm,CD="2" cm,∠DAB="30°,AD=3" cm,试画出它的直观图. 
图1-2-24
图1-2-22是从某一种型号的滚筒洗衣机抽象出来的几何体(单位:cm),试画出它的三视图. 
图1-2-22
如图1-2-13,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点. 
图1-2-13
画出图1-2-11所示几何体的三视图. 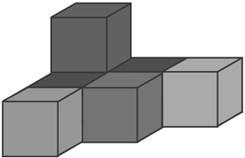
图1-2-11
如图所示,梯形ABCD中,AB∥CD,AB="4" cm,CD="2" cm,∠DAB="30°,AD=3" cm,试画出它的直观图. 