已知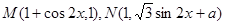
 是常数),且
是常数),且 (
(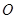 为坐标原点).
为坐标原点).
(1)求 关于
关于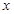 的函数关系式
的函数关系式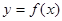 ;
;
(2)若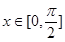 时,
时,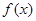 的最大值为4,求
的最大值为4,求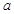 的值;
的值;
(3)在满足(2)的条件下,说明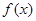 的图象可由
的图象可由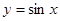 的图象如何变化而得到?
的图象如何变化而得到?
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. 
(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,用
表示这两人参加活动次数之差的绝对值,求随机变量
的分布列及数学期望
.
矩形
的两条对角线相交于点
,
边所在直线的方程为
,点
在
边所在直线上.
(I)求
边所在直线的方程;
(II)求矩形
外接圆的方程;
(III)若动圆
过点
,且与矩形
的外接圆外切,求动圆
的圆心的轨迹方程.
如图,在
中,
,斜边
.
可以通过
以直线
为轴旋转得到,且二面角
是直二面角.动点
的斜边
上.
(I)求证:平面
平面
;
(II)当
为
的中点时,求异面直线
与
所成角的大小;
(III)求
与平面
所成角的最大值.

数列
中,
(
是常数,
),且
成公比不为1的等比数列.
(I)求
的值;
(II)求
的通项公式.
某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为 ,以后每年交纳的数目均比上一年增加 ,因此,历年所交纳的储务金数目 , ,…是一个公差为 的等差数列,与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为 ,那么,在第 年末,第一年所交纳的储备金就变为 ,第二年所交纳的储备金就变为 ,……,以 表示到第 年末所累计的储备金总额.
(Ⅰ)写出
与
的递推关系式;
(Ⅱ)求证:
,其中
是一个等比数列,
是一个等差数列.