已知 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 斜率为
斜率为 的直线
的直线 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于 两点,过
两点,过 且与
且与 垂直的直线
垂直的直线 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于 两点。
两点。
(1)求 的取值范围;
的取值范围;
求四边形 面积的最小值。
面积的最小值。
(本小题满分12分)某普通高中高三年级共有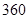 人,分三组进行体质测试,在三个组中男、女生人数如下表所示.已知在全体学生中随机抽取
人,分三组进行体质测试,在三个组中男、女生人数如下表所示.已知在全体学生中随机抽取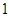 名,抽到第二、三组中女生的概率分别是
名,抽到第二、三组中女生的概率分别是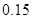 、
、 .
.
| 第一组 |
第二组 |
第三组 |
|
| 女生 |
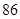 |
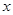 |
 |
| 男生 |
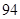 |
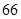 |
 |
(1)求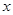 ,
, ,
, 的值;
的值;
(2)为了调查学生的课外活动时间,现从三个组中按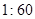 的比例抽取学生进行问卷调查,三个组被选取的人数分别是多少?
的比例抽取学生进行问卷调查,三个组被选取的人数分别是多少?
(3)若从(2)中选取的学生中随机选出两名学生进行访谈,求参加访谈的两名学生“来自两个组”的概率.
(本小题满分12分)已知三棱柱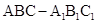 中,侧棱垂直于底面,
中,侧棱垂直于底面,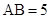 ,
,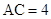 ,
,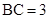 ,
,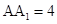 ,点
,点 在
在 上.
上.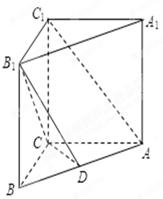
(1)若 是
是 中点,求证:
中点,求证: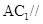 平面
平面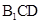 ;
;
(2)当 时,求三棱锥
时,求三棱锥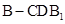 的体积.
的体积.
(本小题满分12分)已知数列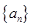 是等差数列,
是等差数列,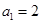 ,
,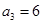 .
.
(1)求数列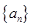 的通项公式;
的通项公式;
(2)设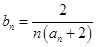 ,求数列
,求数列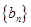 的前
的前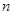 项和
项和 .
.
(本小题满分10分)选修4-5:不等式选讲
设函数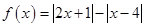 .
.
(1)解不等式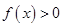 ;
;
(2)若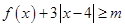 对一切实数
对一切实数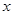 均成立,求
均成立,求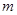 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点,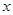 轴的正半轴为极轴建立坐标系.已知曲线
轴的正半轴为极轴建立坐标系.已知曲线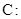
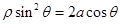 (
(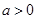 ),过点
),过点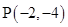 的直线
的直线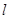 的参数方程为
的参数方程为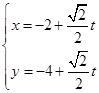 (
(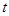 是参数),直线
是参数),直线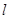 与曲线
与曲线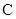 分别交于
分别交于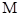 、
、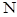 两点.
两点.
(1)写出曲线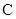 和直线
和直线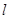 的普通方程;
的普通方程;
(2)若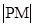 ,
,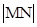 ,
,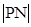 成等比数列,求
成等比数列,求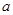 的值.
的值.