已知函数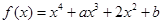 (
(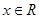 ),其中
),其中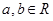 .
.
(Ⅰ)当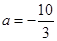 时,讨论函数
时,讨论函数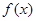 的单调性;
的单调性;
(Ⅱ)若函数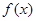 仅在
仅在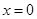 处有极值,求
处有极值,求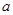 的取值范围;
的取值范围;
(Ⅲ)若对于任意的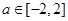 ,不等式
,不等式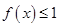 在
在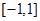 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
已知函数 (
(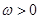 )的最小正周期为
)的最小正周期为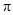 .
.
(1)求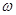 的值;
的值;
(2)求函数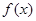 在区间
在区间 上的取值范围.
上的取值范围.
已知集合A= ,B=
,B=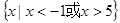 .
.
(1) 若A∩B= ,求实数a的取值范围;
,求实数a的取值范围;
(2) 若A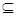 B,求实数a的取值范围.
B,求实数a的取值范围.
正方形ABCD中,点O是对角线AC的中点,点P是对角线AC上一动点.
(1)如图1,当点P在线段OA上运动时(不与点A、O重合) ,PE⊥PB交线段CD于点E,PF⊥CD于点E.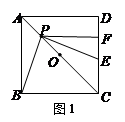
①判断线段DF、EF的数量关系,并说明理由;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
(2)如图2,当点P在线段OC上运动时(不与点O、C重合),PE⊥PB交直线CD于点E,PF⊥CD于点E.判断(1)中的结论①、②是否成立?若成立,说明理由;若不成立,写出相应的结论并证明.
“亚普”塑料厂每月生产甲、乙两种塑料的信息如下表:
| 成本价(元/吨) |
出厂价(元/吨) |
排污处理费(元/吨) |
|
| 甲种塑料 |
800 |
2100 |
200 |
| 乙种塑料 |
1100 |
2400 |
100 |
注1:生产乙种塑料每月还需另外支付专用设备维护费20000元.
注2:总成本包括生产成本、排污处理费、专用设备维护费.
(1)设该厂甲、乙塑料的每月产量分别为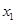 、
、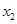 吨,生产利润分别为y1、y2元(生产利润=总收入-总成本),则y1与
吨,生产利润分别为y1、y2元(生产利润=总收入-总成本),则y1与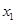 的函数关系式为,y2与
的函数关系式为,y2与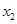 的函数关系式为;
的函数关系式为;
(2)已知该厂每月共生产甲、乙塑料700吨,甲、乙塑料均不超过400吨,求该厂每月生产利润的最大值;
(3)皇冠化学用品销售公司负责销售甲种塑料,试销中发现,甲种塑料销售量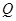 (吨)与销售价
(吨)与销售价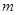 (百元)满足一次函数
(百元)满足一次函数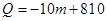 ,营销利润为
,营销利润为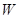 (百元).
(百元).
①求营销利润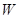 与销售价
与销售价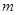 的函数关系式;
的函数关系式;
②当销售价定为多少时,销售甲种塑料营销利润的最大,并求此时的最大利润;
③若规定销售价不低于出厂价,且不高于出厂价的200%,则销售甲种塑料营销利润的最大值是多少?
小明和同桌小聪一起合作探索:如图,一架5米长的梯子AB斜靠在铅直的墙壁AC上,这时梯子的底端B到墙角C的距离为1.4米.如果梯子的顶端A沿墙壁下滑0.8米,那么底端B将向左移动多少米?
(1)小明的思路如下,请你将小明的解答补充完整:
解:设点B将向左移动x米,即BE=x,则:
EC= x+1.4,DC=AC-DC=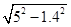 -0.8=4,
-0.8=4,
而DE=5,在Rt△DEC中,由EC2+DC2=DE2,
得方程为:,解方程得:,
∴点B将向左移动米.
(2)解题回顾时,小聪提出了如下两个问题:
①将原题中的“下滑0.8米”改为“下滑1.8米”,那么答案会是1.8米吗?为什么?
②梯子顶端下滑的距离与梯子底端向左移动的距离能相等吗?为什么?
请你解答小聪提出的这两个问题.