小明和同桌小聪一起合作探索:如图,一架5米长的梯子AB斜靠在铅直的墙壁AC上,这时梯子的底端B到墙角C的距离为1.4米.如果梯子的顶端A沿墙壁下滑0.8米,那么底端B将向左移动多少米?
(1)小明的思路如下,请你将小明的解答补充完整:
解:设点B将向左移动x米,即BE=x,则:
EC= x+1.4,DC=AC-DC=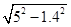 -0.8=4,
-0.8=4,
而DE=5,在Rt△DEC中,由EC2+DC2=DE2,
得方程为: , 解方程得: ,
∴点B将向左移动 米.
(2)解题回顾时,小聪提出了如下两个问题:
①将原题中的“下滑0.8米”改为“下滑1.8米”,那么答案会是1.8米吗?为什么?
②梯子顶端下滑的距离与梯子底端向左移动的距离能相等吗?为什么?
请你解答小聪提出的这两个问题.
“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(下面的临界值表供参考)
 |
0.10 |
0.05 |
0.010 |
0.005 |
 |
2.706 |
3.841 |
6.635 |
7.879 |
(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,
求3名幸运选手中至少有一人在20~30岁之间的概率.
(参考公式: .其中
.其中 .)
.)
某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
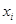 (月) (月) |
 |
 |
 |
 |
 |
 (千克) (千克) |
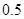 |
 |
 |
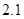 |
 |
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量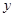 关于变量
关于变量 的线性回归直线方程
的线性回归直线方程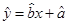 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: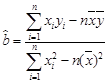 ,
,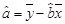 )
)
在三棱锥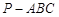 中,
中,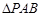 是等边三角形,
是等边三角形,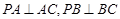 .
.
(1)证明: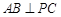 ;
;
(2)若 ,且平面
,且平面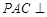 平面
平面 ,求三棱锥
,求三棱锥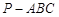 的体积.
的体积.
已知角A、B、C为△ABC的三个内角,其对边分别为a、b、c,若 =(-cos
=(-cos ,sin
,sin ),
), =(cos
=(cos ,sin
,sin ),a=2
),a=2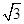 ,且
,且 ·
· =
= .
.
(1)若△ABC的面积S=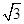 ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范围.
已知函数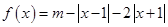
(Ⅰ)当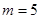 时,求不等式
时,求不等式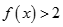 的解集;
的解集;
(Ⅱ)若二次函数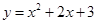 与函数
与函数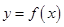 的图象恒有公共点,求实数
的图象恒有公共点,求实数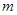 的取值范围.
的取值范围.