(本小题满分16分)如图,在平面直角坐标系 中,已知
中,已知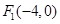 ,
, ,
,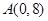 ,直线
,直线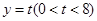 与线段
与线段 、
、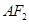 分别交于点
分别交于点 、
、 .
.
(Ⅰ)当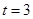 时,求以
时,求以 为焦点,且过
为焦点,且过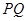 中点的椭圆的标准方程;
中点的椭圆的标准方程;
(Ⅱ)过点 作直线
作直线 ∥
∥ 交
交 于点
于点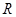 ,记
,记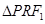 的外接圆为圆
的外接圆为圆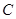 .
.
① 求证:圆心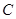 在定直线
在定直线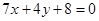 上;
上;
② 圆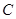 是否恒过异于点
是否恒过异于点 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由. 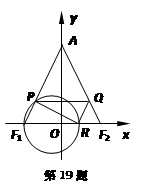
已知函数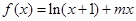 ,当
,当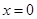 时,函数
时,函数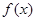 取得极大值.
取得极大值.
(1)求实数 的值;
的值;
(2)已知结论:若函数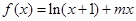 在区间
在区间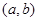 内导数都存在,且
内导数都存在,且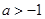 ,则存在
,则存在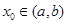 ,使得
,使得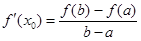 .试用这个结论证明:若
.试用这个结论证明:若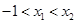 ,函数
,函数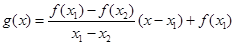 ,则对任意
,则对任意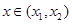 ,都有
,都有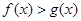 ;
;
(3)已知正数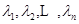 ,满足
,满足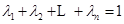 ,求证:当
,求证:当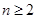 ,
,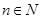 时,对任意大于
时,对任意大于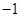 ,且互不相等的实数
,且互不相等的实数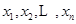 ,都有
,都有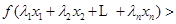
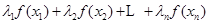 .
.
在直角坐标系 中,动点
中,动点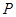 与定点
与定点 的距离和它到定直线
的距离和它到定直线 的距离之比是
的距离之比是 ,设动点
,设动点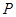 的轨迹为
的轨迹为 ,
,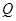 是动圆
是动圆
 上一点.
上一点.
(1)求动点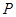 的轨迹
的轨迹 的方程;
的方程;
(2)设曲线 上的三点
上的三点 与点
与点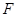 的距离成等差数列,若线段
的距离成等差数列,若线段 的垂直平分线与
的垂直平分线与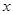 轴的交点为
轴的交点为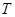 ,求直线
,求直线 的斜率
的斜率 ;
;
(3)若直线 与
与 和动圆
和动圆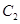 均只有一个公共点,求
均只有一个公共点,求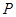 、
、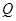 两点的距离
两点的距离 的最大值.
的最大值.
在 中,三个内角
中,三个内角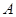 ,
, ,
,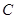 的对边分别为
的对边分别为 ,
, ,
,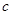 ,其中
,其中 , 且
, 且
(1)求证: 是直角三角形;
是直角三角形;
(2)如图6,设圆 过
过 三点,点
三点,点 位于劣弧上,求
位于劣弧上,求 面积最大值.
面积最大值.
如图5(1)中矩形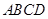 中,已知
中,已知 ,
, ,
, 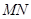 分别为
分别为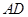 和
和 的中点,对角线
的中点,对角线 与
与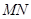 交于
交于 点,沿
点,沿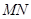 把矩形
把矩形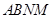 折起,使平面
折起,使平面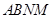 与平面
与平面 所成角为
所成角为 ,如图5(2).
,如图5(2).
(1)求证: ;
;
(2)求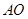 与平面
与平面 所成角的正弦值.
所成角的正弦值.

有一个3×4×5的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成60个1×1×1的小正方体,从这些小正方体中随机地任取1个,设小正方体涂上颜色的面数为 .
.
(1)求 的概率;
的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.