(本题12分)△ABC中,∠A=∠B=30°,AB=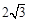 .把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O (如图),△ABC可以绕点O作任意角度的旋转.
.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O (如图),△ABC可以绕点O作任意角度的旋转.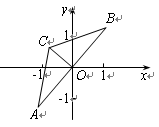
(1) 当点B在第一象限,纵坐标是
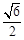 时,求点B的横坐标;
时,求点B的横坐标;(2) 如果抛物线
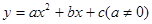 的对称轴经过点C,请你探究:
的对称轴经过点C,请你探究:
①当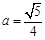 ,
,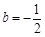 ,
,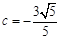 时,A,B两点是否都在这条抛物线上?并说明理由;
时,A,B两点是否都在这条抛物线上?并说明理由;
②设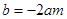 ,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
出租车司机小石某天下午营运全是在东西走向的人民大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-3,+14,-11,+10,-12.
(1)将最后一名乘客送达目的地时,小石距下午出发地点的距离是多少千米?
(2)若汽车耗油量为0.3升/千米,这天下午汽车耗油共多少升?
已知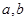 互为倒数,
互为倒数,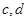 互为相反数,
互为相反数,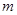 的绝对值为2,求
的绝对值为2,求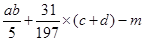 的值
的值
(1)若我们把不小于x的最小整数记作〈x〉,如〈2.4〉=3,〈-1.5〉=-1;则〈3〉= ,〈-2.2〉=
(2)在我国,出租车已经普及,杭州城区A、B两种出租车,它们的收费方式有所不同, A种出租车的收费方式是:每千米收费2.5元,不收其它费用。B种出租车的收费方式是:行程不超过3千米收费8元,超过3千米后超出部分每千米再增收2元,同时每趟营运在计价器显示的金额外再向乘客加收1元的燃料附加费.(注:两种出租车在路程上不足1千米按1千米计算,如6.1千米应算成7千米)若某公司员工小王需要乘出租车到离家x千米的公司上班。
①请利用题(1)中的符号,用代数式表示小王分别使用A、B两种出租车的收费情况。
②分别求出x=4.5;x=6;x=6.1时A、B两种出租车的收费情况.
③结合②的答案请说一说小王为了省钱应该如何选择出租车。
某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有 张桌子时,两种摆放方式各能坐多少人?
张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
出租车司机小张某天上午营运全是在东西走向的政府大道上进行的,如果规定向东为正,向西为负,他这天上午的行程是(单位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距上午出发点的距离是多少千米?在出发点的什么方向?
(2)若汽车耗油量为0.6升/千米,出车时,邮箱有油72.2升,若小张将最后一名乘客送达目的地,再返回出发地,问小张今天上午是否需要加油?若要加油至少需要加多少才能返回出发地?若不用加油,请说明理由。