20世纪90年代,气候变化专业委员会向政府提供的一项报告指出:全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐中使CO2体积分数增加。据测,1990年、1991年、1992年大气中的CO2体积分数分别比1989年增加了1个可比单位、3个可比单位、6个可比单位。若用一个函数模拟20世纪90年代中每年CO2体积分数增加的可比单位数 与年份增加数
与年份增加数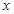 (即当年数与1989的差)的关系,模拟函数可选用二次函数
(即当年数与1989的差)的关系,模拟函数可选用二次函数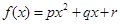 (其中
(其中 为常数)或函数
为常数)或函数 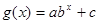 (其中
(其中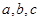 为常数,且
为常数,且 ),(1)根据题中的数据,求
),(1)根据题中的数据,求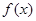 和
和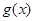 的解析式;(2)如果1994年大气中的CO2体积分数比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数较好?并说明理由。
的解析式;(2)如果1994年大气中的CO2体积分数比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数较好?并说明理由。
已知函数 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, ,
, ∈R.
∈R.
(1)求θ的值;
(2)若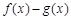 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设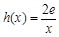 ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得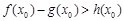 成立,求
成立,求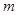 的取值范围.
的取值范围.
已知数列 满足
满足 ,且
,且 ,
,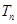 为
为 的前
的前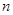 项和.
项和.
(1)求证:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(2)如果对于任意 ,不等式
,不等式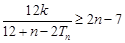 恒成立,求
恒成立,求 实数
实数 的取值范围.
的取值范围.
已知函数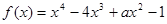 在区间[0,1]上单调递增,在区间[1,2]上单调递减。
在区间[0,1]上单调递增,在区间[1,2]上单调递减。
(1)求 的值;
的值;
(2)若斜率为24的直线是曲线 的切线,求此直线方程;
的切线,求此直线方程;
(3)是否存在实数b,使得函数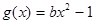 的图象与函数
的图象与函数 的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
集合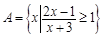 ,
,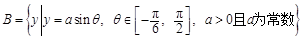 .
.
(1)求集合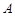 和B;
和B;
(2)若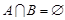 ,求
,求 的取值范围
的取值范围
已知
(1)求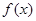 的周期,并求
的周期,并求 时的单调增区间.
时的单调增区间.
(2)在△ABC中,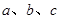 分别是角A,B,C所对的边,若
分别是角A,B,C所对的边,若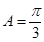 ,且
,且 ,求
,求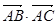 的最大值.
的最大值.