我市有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.某公司准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.(1)设在甲家租一张球台开展活动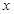 小时的收费为
小时的收费为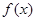 元
元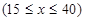 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动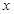 小时的收费为
小时的收费为 元
元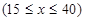 ;试求
;试求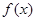 和
和 ;(2)问:选择哪家比较合算?为什么?
;(2)问:选择哪家比较合算?为什么?
(本小题满分16分)若数列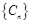 满足①
满足①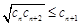 ,②存在常数
,②存在常数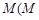 与
与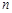 无关),使
无关),使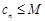 .则称数列
.则称数列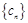 是“和谐数列”.
是“和谐数列”.
(1)设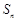 为等比数列
为等比数列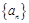 的前
的前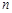 项和,且
项和,且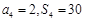 ,求证:数列
,求证:数列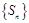 是“和谐数列”;
是“和谐数列”;
(2)设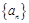 是各项为正数,公比为q的等比数列,
是各项为正数,公比为q的等比数列,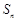 是
是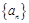 的前
的前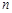 项和,求证:数列
项和,求证:数列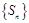 是“和谐数列”的充要条件为
是“和谐数列”的充要条件为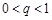 .
.
(本小题满分16分)已知函数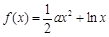 ,
,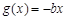 ,设
,设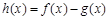 .
.
(1)若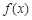 在
在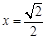 处取得极值,且
处取得极值,且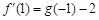 ,求函数h(x)的单调区间;
,求函数h(x)的单调区间;
(2)若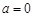 时函数h(x)有两个不同的零点x1,x2.
时函数h(x)有两个不同的零点x1,x2.
①求b的取值范围;②求证: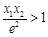 .
.
(本小题满分16分) 已知椭圆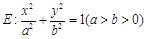 过点
过点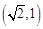 ,离心率为
,离心率为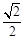 .
.
(1)若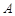 是椭圆
是椭圆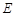 的上顶点,
的上顶点,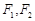 分别是左右焦点,直线
分别是左右焦点,直线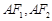 分别交椭圆于
分别交椭圆于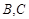 ,直线
,直线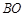 交
交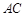 于D,求证
于D,求证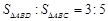 ;
;
(2)若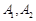 分别是椭圆
分别是椭圆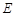 的左右顶点,动点
的左右顶点,动点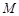 满足
满足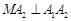 ,且
,且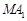 交椭圆
交椭圆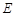 于点
于点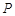 .
.
求证: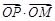 为定值.
为定值.
(本小题满分14分)2014年8月以“分享青春,共筑未来”为口号的青奥会在江苏南京举行,
为此某商店经销一种青奥会纪念徽章,每枚徽章的成本为30元,并且每卖出一枚徽章需向相关部门上缴 元(
元( 为常数,
为常数, ),设每枚徽章的售价为
),设每枚徽章的售价为 元(35
元(35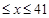 ).根据市场调查,日销售量与
).根据市场调查,日销售量与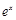 (
(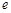 为自然对数的底数)成反比例.已知当每枚徽章的售价为40元时,日销售量为10枚.
为自然对数的底数)成反比例.已知当每枚徽章的售价为40元时,日销售量为10枚.
(1)求该商店的日利润 与每枚徽章的售价
与每枚徽章的售价 的函数关系式;
的函数关系式;
(2)当每枚徽章的售价为多少元时,该商店的日利润 最大?并求出
最大?并求出 的最大值.
的最大值.
(本小题满分14分)在四棱锥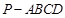 中,
中,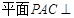 平面
平面 ,
,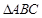 是边长为4的正三角形,
是边长为4的正三角形,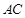 与
与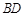 的交点
的交点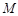 恰好是
恰好是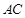 中点,又
中点,又 ,点
,点 在线段
在线段 上,且
上,且 .
.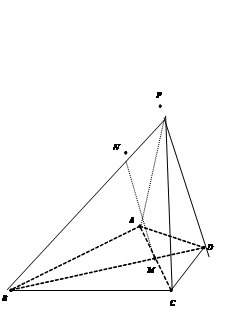
(1)求证: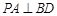 ;
;
(2)求证: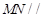 平面
平面 .
.