已知,椭圆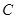 经过点
经过点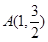 ,两个焦点的坐标为
,两个焦点的坐标为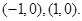
(Ⅰ)求椭圆 的方程;(Ⅱ)
的方程;(Ⅱ) 是椭圆
是椭圆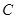 上的两个动点,如果直线
上的两个动点,如果直线 的斜率与
的斜率与 的斜率互为相反数,证明:直线
的斜率互为相反数,证明:直线 的斜率为定值,并求出这个定值。
的斜率为定值,并求出这个定值。
已知函数
(1)判断 的奇偶性
(2)若 在 是增函数,求实数 的范围.
近年来,太阳能技术运用的步伐日益加快,已知
年全球太阳能年生产量为
兆瓦,年增长率为
。在此后的四年里,增长率以每年
的速度增长(例如2003年的年生产量增长率为
)
(1)求
年的太阳能年生产量(精确到
兆瓦)
(2)已知
年太阳能年安装量为
兆瓦,在此后的
年里年生产量保持
的增长率,若
年的年安装量不少于年生产量的
,求
年内年安装量的增长率的最小值(精确到
)
在三角形 中, , , ,求三角形 的面积 .
体积为1的直三棱柱 中, ,求直线 与平面 所成角.
已知各项全不为零的数列
的前k项和为
,且
,其中
.
(Ⅰ)求数列
的通项公式;
(Ⅱ)对任意给定的正整数
,数列
满足
.求
.