如图1,正方形ABCD和正方形QMNP,∠M =∠B,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E.求证:ME = MF.
如图2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME与线段MF的关系,并加以证明.
如图3,若将原题中的“正方形”改为“矩形”,且AB = mBC,其他条件不变,探索线段ME与线段MF的关系,并说明理由.
根据前面的探索和图4,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题;若不能,请说明理由

如图已知AB是 的切线,切点为
的切线,切点为 交
交 于点
于点 过点
过点 作
作 交
交 于点
于点
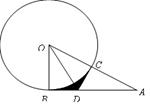
求证:
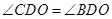 ;
;若
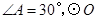 的半径为4,求CD的长;
的半径为4,求CD的长;求阴影部分的面积。
如图,已知抛物线C1: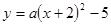 的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.求P点坐标及a的值;
如图(1),

抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;如图(2),

点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.如图1,当∠ABC=45°时,求证:AE=
 MD;
MD;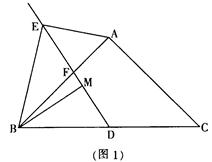
如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为:。
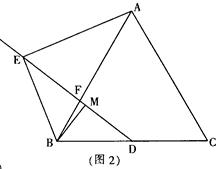
在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=
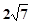 ,求tan∠ACP的值.
,求tan∠ACP的值.
某州有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售.设
 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为 元,试写出
元,试写出 与
与 之间的函数关系式
之间的函数关系式若存放
 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为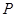 元,试写出
元,试写出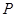 与
与 之间的函数关系式.
之间的函数关系式.李经理将这批野生茵存放多少天后出售可获得最大利润
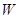 元?
元?
(利润=销售总额-收购成本-各种费用).