(本小题满分12分) (1)观察发现
如(a)图,若点A,B在直线 同侧,在直线
同侧,在直线 上找一点P,使AP+BP的值最小.
上找一点P,使AP+BP的值最小.
做法如下:作点B关于直线 的对称点
的对称点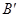 ,连接
,连接 ,与直线
,与直线 的交点就是所求的点P
的交点就是所求的点P
再如(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 . (2分)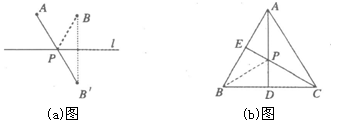
(2)实践运用
如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,求PM+PN的最小值。(5分)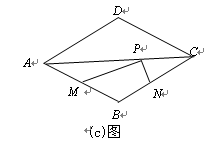
(3)拓展延伸
如(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留作图痕迹,不必写出作法. (5分)
为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为 、 、 、 四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:

(1) , , ;
(2)扇形统计图中表示 等次的扇形所对的圆心角的度数为 度;
(3)学校决定从 等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
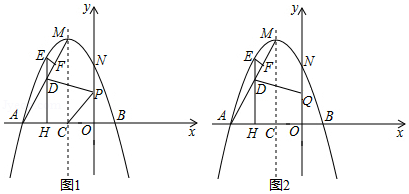
在平面直角坐标系中,抛物线 与 轴交于点 、 ,交 轴于点 ,点 为抛物线的顶点,对称轴与 轴交于点 .
(1)求抛物线的解析式;
(2)如图1,连接 ,点 是线段 上方抛物线上一动点, 于点 ,过点 作 轴于点 ,交 于点 .点 是 轴上一动点,当 取最大值时:
①求 的最小值;
②如图2, 点为 轴上一动点,请直接写出 的最小值.
如图, 是 的外接圆, 为直径,点 为 外一点,且 ,连接 交 于点 ,延长 交 于点 .
(1)证明: ;
(2)若 ,证明: 是 的切线;
(3)在(2)条件下,连接 交 于点 ,连接 ,若 ,求 的长.

我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.例如,代数式 的几何意义是数轴上 所对应的点与2所对应的点之间的距离:因为 ,所以 的几何意义就是数轴上 所对应的点与 所对应的点之间的距离.
(1)发现问题:代数式 的最小值是多少?
(2)探究问题:如图,点 、 、 分别表示数 、2、 , .

的几何意义是线段 与 的长度之和,
当点 在线段 上时, ,当点 在点 的左侧或点 的右侧时, .
的最小值是3.
(3)解决问题:
① 的最小值是 ;
②利用上述思想方法解不等式: ;

③当 为何值时,代数式 的最小值是2.
甲、乙两家商场平时以同样价格出售相同的商品.新冠疫情期间,为了减少库存,甲、乙两家商场打折促销.甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.
(1)以 (单位:元)表示商品原价, (单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数解析式;
(2)新冠疫情期间如何选择这两家商场去购物更省钱?