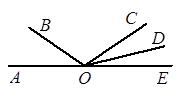.(本小题满分12分)
如图,已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连结AF交CE于H,连结AC、CF、BF。
(1)请你找出图中的相似三角形,并对其中的一对相似三角形进行证明;
(2)若AE:BE=1:4,求CD长。
(3)在(2)的条件下,求
 的值。
的值。
先化简,再求值:9a2b+ (-3ab2)-(3a2b-4ab2),其中a=-3, .
.
解下列方程:
(1) ;
;
(2) .
.
(本题12分)某检修小组乘汽车沿公路检修线路,约定往东为正,往西为负.某天自A地出发到收工时所走路线(单位:千米)为:-10,-3,+4,+2,-8,+13,-2,-12,+8,+5.
(1)问收工时距A地多远?在哪个方向?
(2)若每千米路程耗油m升,问从A地出发到收工共耗油多少升?
小王买了50元的乘车月票卡,如果小王乘车的次数用n表示,则记录他每次乘车后的余额m(元)如下表:
| 次数 |
余额m(元) |
| 1 |
50-0.8 |
| 2 |
50-1.6 |
| 3 |
50-2.4 |
| 4 |
50-3.2 |
| … |
… |
(1)写出用乘车的次数n表示余额m的式子.
(2)利用上式计算乘了13次车后,余额为多少?
(3)小王最多能乘几次车?
(本题12分)如图,点A、O、E在同一直线上,∠AOB=40°,∠EOD=28°46′,OD平分∠COE, 求∠COB的度数.