如图,已知△ABC中,∠B="90" º,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形?
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.
如图,CD∥AB,∠ABC,∠BCD的角平分线交于E点,且E在AD上,CE交BA的延长线于F点。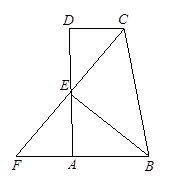
(1)BE与CF互相垂直吗?若垂直,请说明理由;
(2)若CD=3,AB=4,求BC的长.
.八年级数学活动小组为了调查居民的用水情况,从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如 下表所示:
下表所示:
| 月用水量(吨) |
3 |
4 |
5 |
7 |
8 |
9 |
10 |
| 户数 |
4 |
3 |
5 |
11 |
4 |
2 |
1 |
(1)求这30户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为m(吨),家庭月用水量不超过m(吨)的部分按原价收费,超过m(吨)的部分加倍收费。你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由。
“中华人民共和国道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直通行驶到车速检测仪A的正前方30米C处,过了2秒后行驶到B处,此时测得小汽车与车速成检测仪间距离为50米,这辆小汽车超速了吗?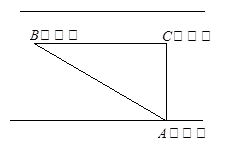
画图:⑴马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如下图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子。
(注:①只需添加一个符合要求的正方形;
②添加的正方形用阴影表示。) 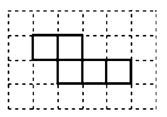
⑵如 图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:
图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图: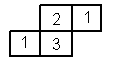
主视图左视图