如图,已知点F(2,0),点P在y 轴上运动,过P作PM⊥PF交x轴于M,延长MP到点N,使|PN|=|PM|.
⑵ 求动点N的轨迹C的方程;
⑵在⑴中所求的曲线C上有三点A(x1,y1),B(x2,y2),D(x3,y3),若|AF|、|BF|、|DF|成等差数列,且线段AD的中垂线与x轴的交点为(6,0),求点B的坐标。
某兴趣小组要测量电视塔AE的高度H(单位:m).如示意图,垂直放置的标杆BC的高度h=4 m,仰角∠ABE=α,∠ADE=β.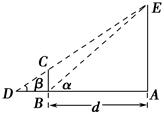
(1)该小组已测得一组α,β的值,算出了tan α=1.24,tan β=1.20,请据此算出H的值;
(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125 m,试问d为多少时,α-β最大?
已知函数f(x)=sin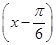 +cosx-
+cosx- ,g(x)=2sin2
,g(x)=2sin2 .
.
(1)若α是第一象限角,且f(α)=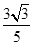 .求g(α)的值;
.求g(α)的值;
(2)求使f(x)≥g(x)成立的x的取值集合.
已知函数f(x)=sin 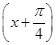 ·sin
·sin  +
+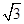 sin xcos x(x∈R).
sin xcos x(x∈R).
(1)求f 的值;
的值;
(2)在△ABC中,若f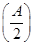 =1,求sin B+sin C的最大值.
=1,求sin B+sin C的最大值.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的图象的一部分如图所示.
)的图象的一部分如图所示.
(1)求函数f(x)的解析式;
(2)当x∈ 时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
已知函数f(x)=ex-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.