已知二次函数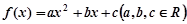 ,
,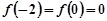 ,
,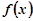 的最小值为
的最小值为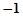 .
.
(1)求函数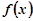 的解析式;
的解析式;
(2)设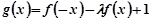 ,若
,若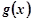 在
在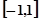 上是减函数,求实数
上是减函数,求实数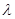 的取值范围;
的取值范围;
(3)设函数 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数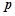 的取值范围.
的取值范围.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
函数 的一段图象如图所示.
的一段图象如图所示.
(1)求函数 的解析式;
的解析式;
(2)将函数 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到 的图象,求直线
的图象,求直线 与函数
与函数 的图象在
的图象在 内所有交点的坐标.
内所有交点的坐标.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组: ,
, ,
, 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
(Ⅰ)求图中实数 的值;
的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在 与
与 两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
先后随机投掷2枚正方体骰子,其中 表示第
表示第 枚骰子出现的点数,
枚骰子出现的点数, 表示第
表示第 枚骰子出现的点数.
枚骰子出现的点数.
(Ⅰ)求点 在直线
在直线 上的概率;
上的概率;
(Ⅱ)求点 满足
满足 的概率.
的概率.