已知四棱锥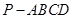 的底面为直角梯形,
的底面为直角梯形,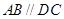 ,
, 底面
底面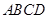 ,且
,且 ,
,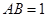 ,
,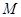 是
是 的中点。
的中点。
(Ⅰ)证明:面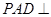 面
面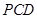 ;
;
(Ⅱ)求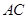 与
与 所成的角的余弦值;
所成的角的余弦值;
(Ⅲ)求面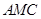 与面
与面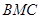 所成二面角的余弦值。
所成二面角的余弦值。
设函数 (其中
(其中 ),
), ,已知它们在
,已知它们在 处有相同的切线.
处有相同的切线.
(1)求函数 ,
, 的解析式;
的解析式;
(2)求函数 在
在 上的最小值;
上的最小值;
(3)判断函数 零点个数.
零点个数.
如图,矩形 所在的平面和平面
所在的平面和平面 互相垂直,等腰梯形
互相垂直,等腰梯形 中,
中, ∥
∥ ,
, =2,
=2, ,
, ,
, ,
, 分别为
分别为 ,
, 的中点,
的中点, 为底面
为底面 的重心.
的重心.
(1)求证:平面 平面
平面 ;
;
(2)求证:  ∥平面
∥平面 ;
;
(3)求多面体 的体积
的体积 .
.
已知正项数列 ,其前
,其前 项和
项和 满足
满足 且
且 是
是 和
和 的等比中项..
的等比中项..
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前99项和.
的前99项和.
某单位招聘职工,经过几轮筛选,一轮从2000名报名者中筛选300名进入二轮笔试,接着按笔试成绩择优取100名进入第三轮面试,最后从面试对象中综合考察聘用50名.
(1)求参加笔试的竞聘者能被聘用的概率;
(2)用分层抽样的方式从最终聘用者中抽取10名进行进行调查问卷,其中有3名女职工,求被聘用的女职工的人数;
(3)单位从聘用的三男和二女中,选派两人参加某项培训,至少选派一名女同志参加的概率是多少?
已知向量 ,
, .
.
(1)若 ,
, ,且
,且 ,求
,求 ;
;
(2)若 ,求
,求 的取值范围.
的取值范围.