设函数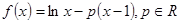 .
.
(Ⅰ)当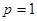 时,求函数
时,求函数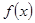 的单调区间;
的单调区间;
(Ⅱ)设函数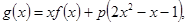 对任意
对任意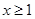 都有
都有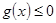 成立,求
成立,求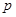 的取值范围.
的取值范围.
在高二年级中的8个班,组织一个12个人的年级学生分会,每班要求至少1人,名额分配方案有多少种?
将4个相同的白球、5个相同的黑球、6个相同的红球放入4个不同的盒子中的3个中,使得有一个空盒且其他盒子中球的颜色齐全的不同放法有多少种?
把20个相同的球全放入编号分别为1,2,3的三个盒子中,要求每个盒子中的球数不少于其编号数,则有多少种不同的放法?
10个三好学生名额分到7个班级,每个班级至少一个名额,有多少种不同分配方案?
(1)有4名学生报名参加数学、物理、化学竞赛,每人限报一科,有多少种不同的报名方法?
(2)有4名学生参加争夺数学、物理、化学竞赛冠军,有多少种不同的结果?
(3)将3封不同的信投入4个不同的邮筒,则有多少种不同投法?