在高二年级中的8个班,组织一个12个人的年级学生分会,每班要求至少1人,名额分配方案有多少种?
已知抛物线
上有两点
（1）当抛物线的准线方程为
时，作正方形ABCD使得边CD直线方程为
，求正方形
的边长；
（2）抛物线上一定点Px0，，y0）（y0>0），当PA与PB的斜率存在且倾斜角互补时，求证直线AB的斜率是非零常数．
如图所示，已知圆O1与圆O2外切，它们的半径分别为4、2，圆C与圆O1、圆O2外切．
（1）建立适当的坐标系，求圆C的圆心的轨迹方程；
（2）在（1）的坐标系中，若圆C的半径为3，求圆C的方程．
已知三角形的三个顶点坐标分别为：点A（0，1）、B（4，-1）、C（2，5）
（1）若经过点A的直线l与点B和点C的距离相等，求直线l的方程；
（2）若点
是
外接圆上的动点，求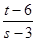
的取值范围．
中心在原点，焦点在坐标轴上的一个椭圆与一双曲线有共同的焦点F1，F2，且
，椭圆的长半轴比双曲线的半实轴长
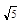，离心率之比为2：3。求这两条曲线的方程。
已知中心在原点，焦点在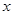
轴的椭圆过点
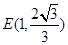，且焦距为2，过点
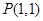分别作斜率为
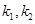的椭圆的动弦
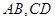，设
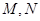分别为线段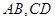的中点．
（1）求椭圆的标准方程；
（2）若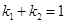
，求证：直线
恒过定点，并求出定点坐标．